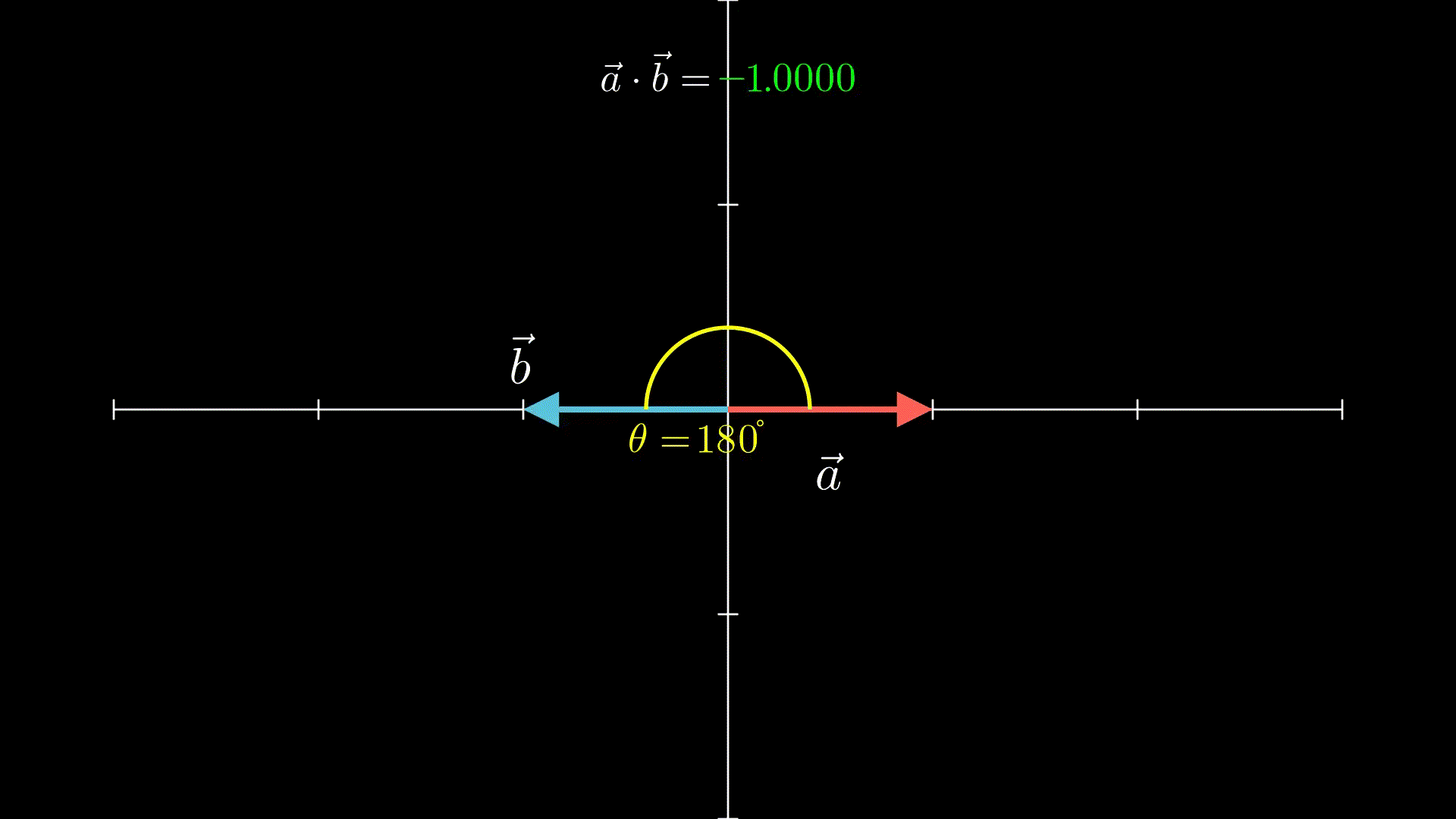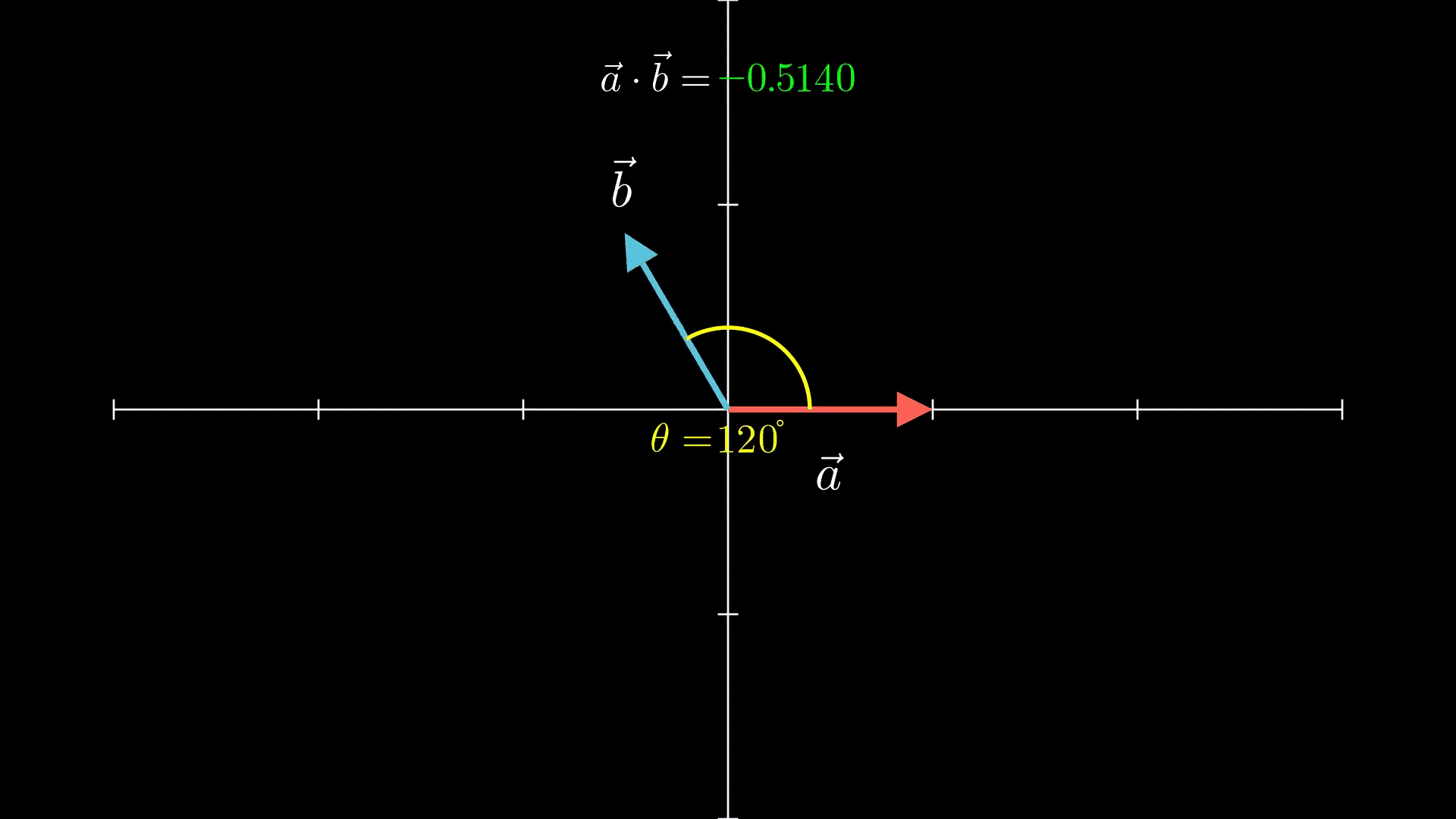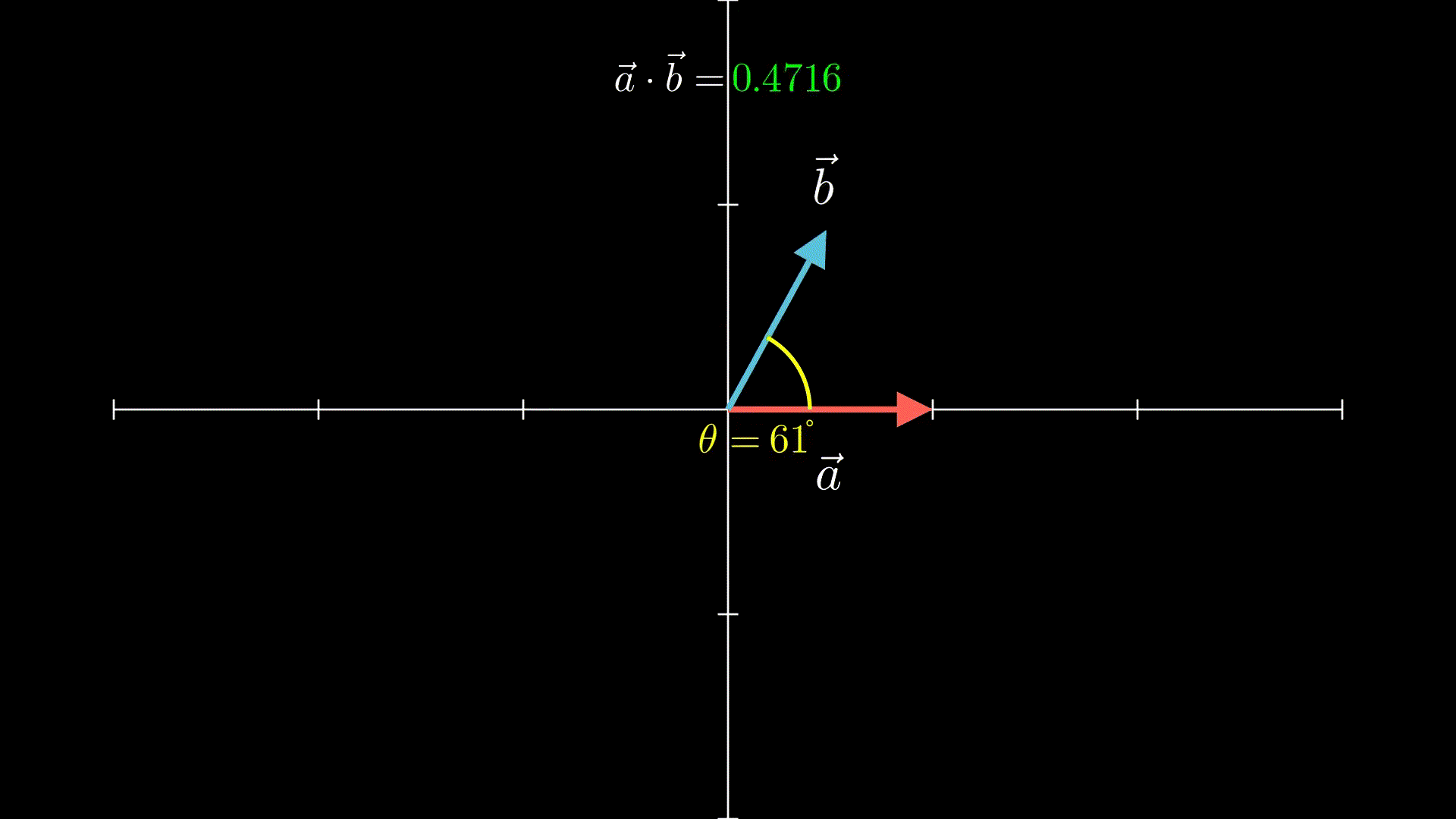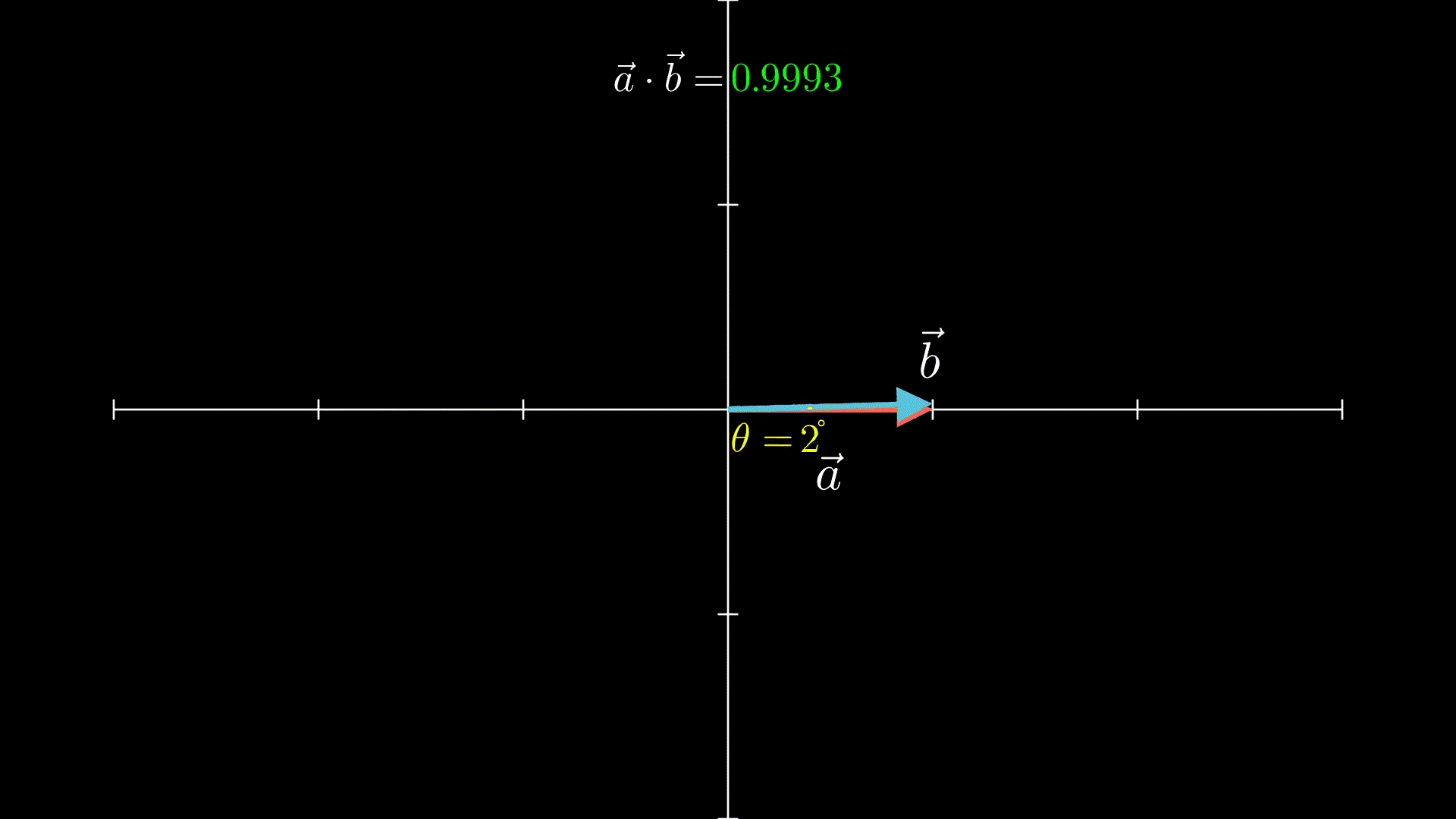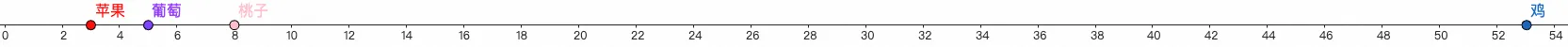建议电脑观看
⚠️⚠️⚠️ 如果发现公式渲染不对，请刷新下页面，渲染经常抽风

前言

最近各种AI Agent、MCP、A2A、RAG横空出世，搞得正在写神经网络、Transformer的我好像在开倒车一样，多少是有点焦虑🥲，不过既然头都开起来了，还是把坑填完吧= =
这里先声明文章面向对象：
- 主要是面向非算法专业的同学，基础已经比较扎实的估计对你没啥帮助/提升
- 会涉及一丢丢数学，但已经最简单化，相信在座各位都能看懂
- 好消息是不需要代码基础🥳，坏消息是有代码基础也没什么卵用🤪
你能收获什么：
- 初步了解什么是神经网络、激活函数等基础概念
- 多少能"意会"到transformer乃至大模型的文本是怎么生成出来的
难度曲线：

必要基础

从预测酒店销量开始

🌴 这个case原版是房价预测，这里稍微改成酒店更贴合业务（

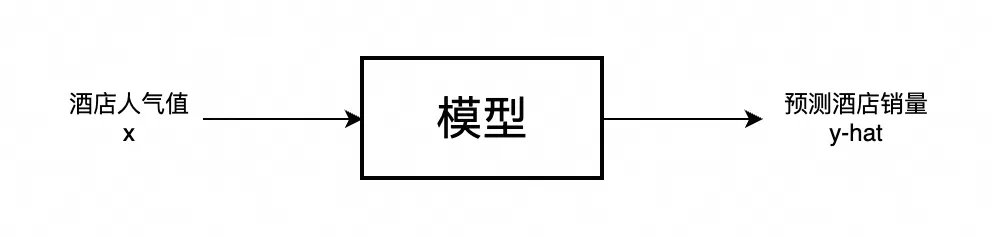
假设现在想通过机器学习的方式，预测一下不同酒店在某个时刻的销量，我们需要先定义一个简单的函数，它能做到以下功能：
实际上你也可以将f看成模型（model），如下图所示：

我们可以先使用一个简单的线性回归，来做作为这个模型的实现，方程为： $y=wx+b$
- 假设用来训练的酒店有n家，那么第一家酒店的人气值表示为： $x_1$
- 第一家酒店的实际价格表示为： $y_1$
- 模型预测时的权重就是w(widget)，偏置是b(bias)，这两一开始都是随机值
- 通过 $wx_1+b$ 预测第一家酒店的的结果为： $y_{hat}$
函数示例动画如下：

衡量好坏

有了模型后，我们自然需要衡量这个模型的好坏，从上个例子中可以使用一种简单的方式算这个好坏： $lose_1=|y_{hat1}-y_1|$
$lose_1$ 随着w、b变化如下所示：
当然，这里只是衡量一家酒店，如果是2家酒店，就会变成这个样子：
- 至于酒店变成3、4家，为了画面整洁我就不继续扩下去了，还请自行脑补一下
最终衡量n家酒店好坏就是： $L=\sum_{i=1}^{n} lose_i$
如果将画出 $w$ 和 $L$ 的关系函数，大概长下面这个样子：
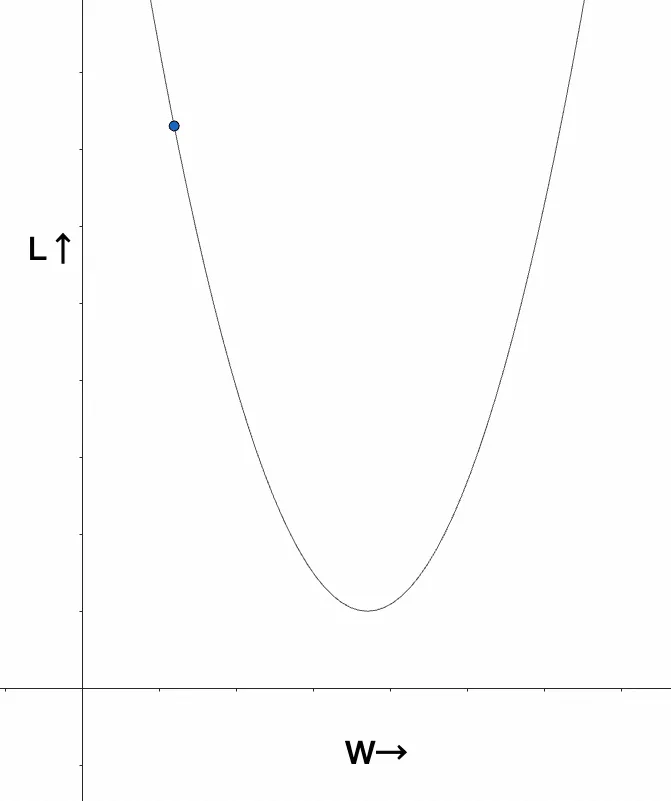
- 图中暂时忽略了b的作用，这个不关键
不难看出，如果想要模型的准确率最高，就需要把w更新成L最低的位置
那么，问题来了：前面提到w、b是随机设置的值，要如何让w自动调节，使得L最低？

梯度下降

要解决上面的问题，就不得不提到梯度下降（也叫自动求导）
如果你忘了高数学的导数/微分，也没有关系，你只需要知道求导实际上在算某个点的斜率就行
斜率k随w的变化如下所示：
可以看到，要让w向L最低点更新，需要让w减k（ $导数形式：w-\frac{dL}{dw}$ ）
但，通常我们不会让w直接减去斜率，否则可能出现如下情况：
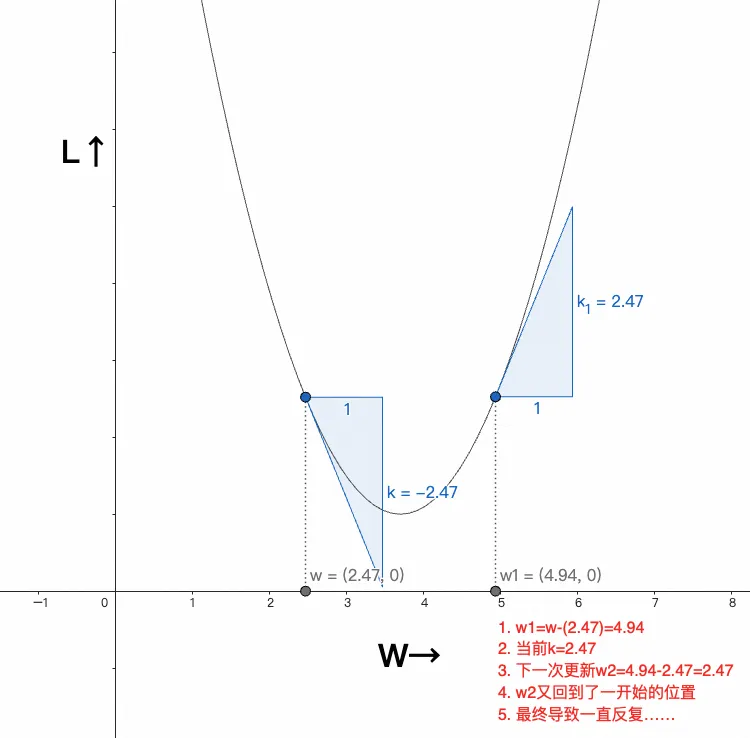
- 说白了就是无法到达L的最低点
所以通常会引入一个叫学习率（ $\alpha$ ）的变量，于是式子变成： $w-\alpha\frac{dL}{dw}$
w每次变化的幅度表示为 $\Delta w$ ，假设 $\alpha=0.5$ ，整个梯度下降的过程将如下所示：
到这里，相信你已经对梯度下降有了一个非常直观的了解，只不过现在是从2D的角度，毕竟现在只有人气值这一个维度去预测销量
如果加设施数量，再将梯度下降进行可视化，可能就是下面这个样子：
到这里可能会有人问，如果再增加一个维度做4D可视化呢？唔...很遗憾，至少我做不到，这也是为啥在这个领域为啥有些问题很难解释，就算最后通过各种手段可视化，也只有专业人员才能看懂
小结：实际上训练的过程也就是对无数 $w_n$ 、 $b_n$ 进行调整，让 $L$ 尽可能下降

✍🏻 ✍🏻 ✍🏻
总的来说，梯度下降是是训练模型的重要算法，除了梯度下降外，还有很多算法，比如：如何调整动态学习率？如何在复杂神经网络中找出对lose影响最大的w、b，并更新到合适的值（反向传播）等等
而在这里，我并不打算把这些细枝末节都一个个讲清楚，因为本文的目的是以最少的成本去理解Transformer，有些内容即便不知道也不妨碍理解
如果你对反向传播这种"入门劝退"级别的内容感兴趣（建议还存有一部分微积分记忆），那么我建议是看这个：Bilibili-李沐-07 自动求导（注意，这不是0基础入门内容）

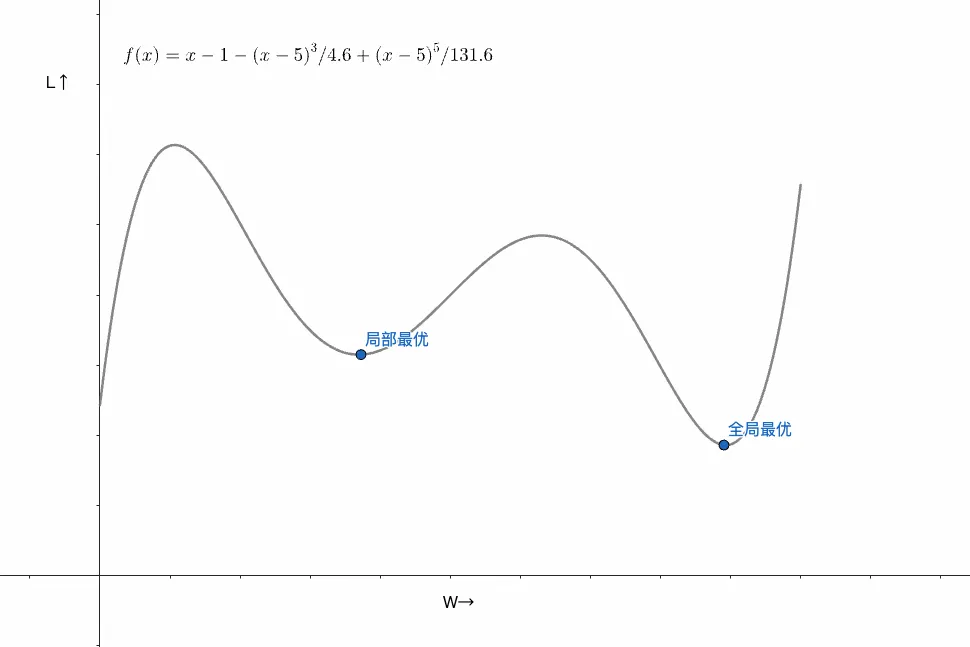
局部最优和全局最优

上面的case的L和w的函数图都是一个U型，但实际训练的时候往往不止1个低点，往往在一定区间内非L值最低的点叫做局部最优（可以有多个），而全局L最低的地方叫全局最优，如下图所示：

至于如何逃离局部最优，逼近全局最优，这又是另外一个很大的问题，在这里不再展开

非线性问题 + 激活函数

现在回过头来看文章开头的例子，似乎有点简单了，因为人气和销量几乎成正比，所以一个线性函数通过不断调整w、b就能的到一个还行的预测模型
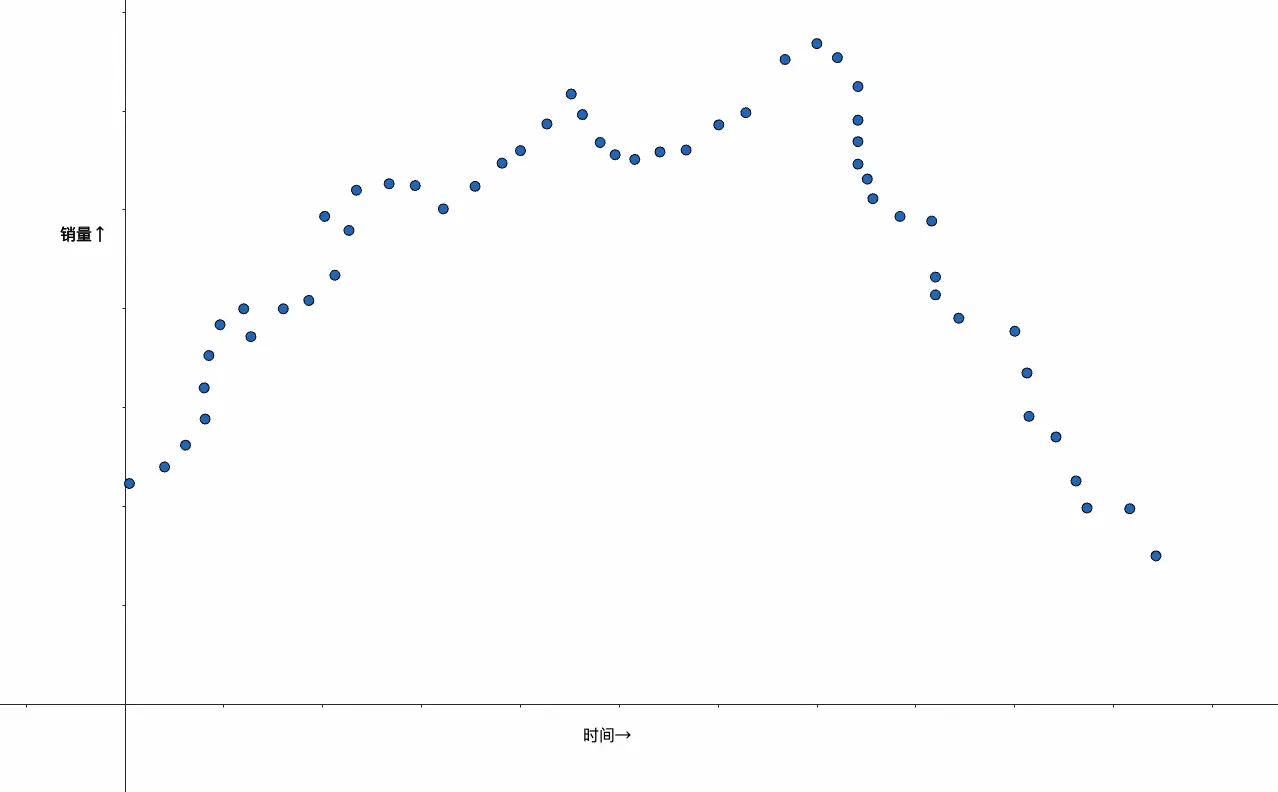
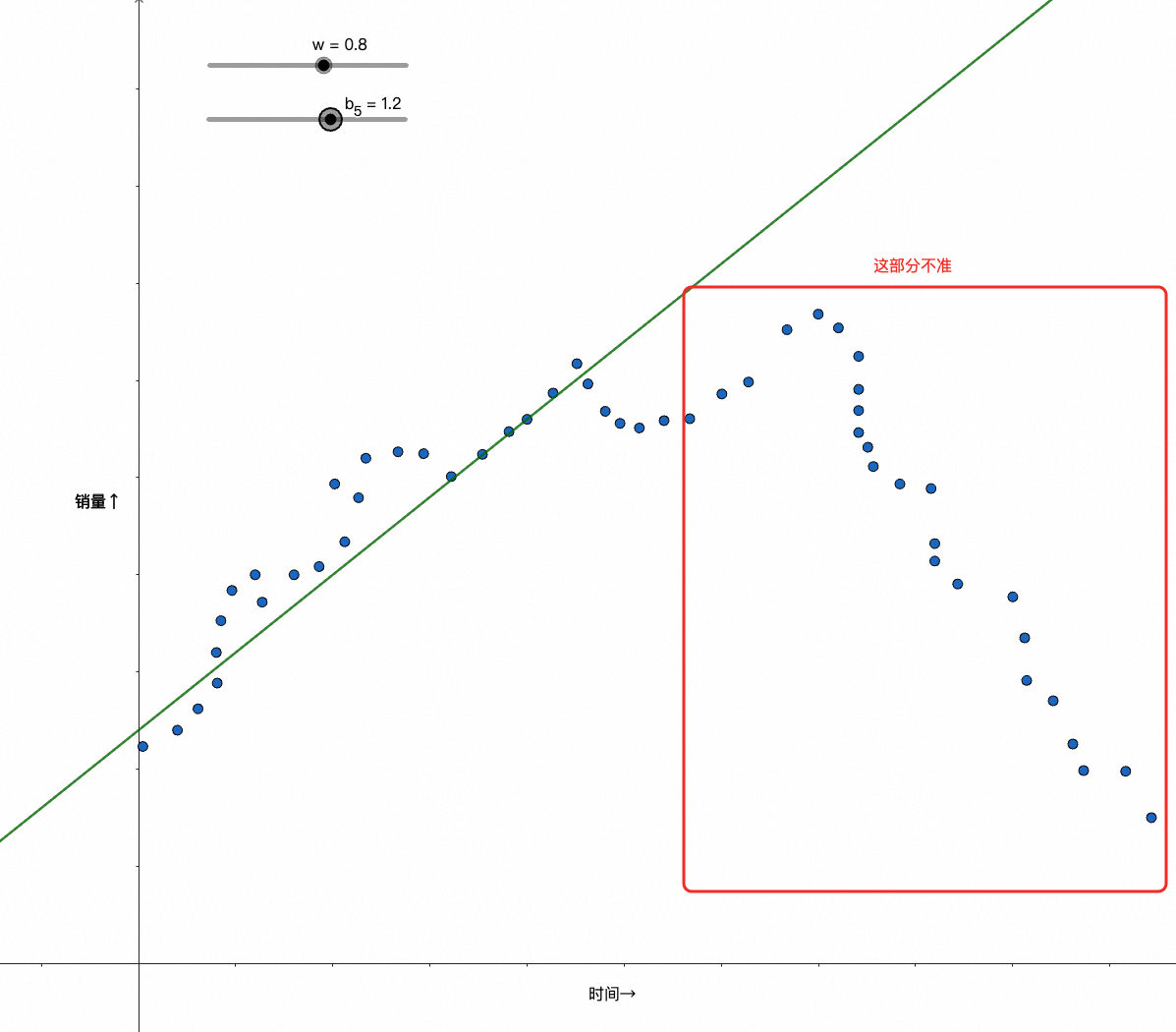
但如果不是用人气去预测销量，而是用时间呢？比如0点到24点，那么数据分布可能是下面这样的：
此时我们很难再通过wx+b的纯线性模型去较好地拟合数据了，比如像下面的case：
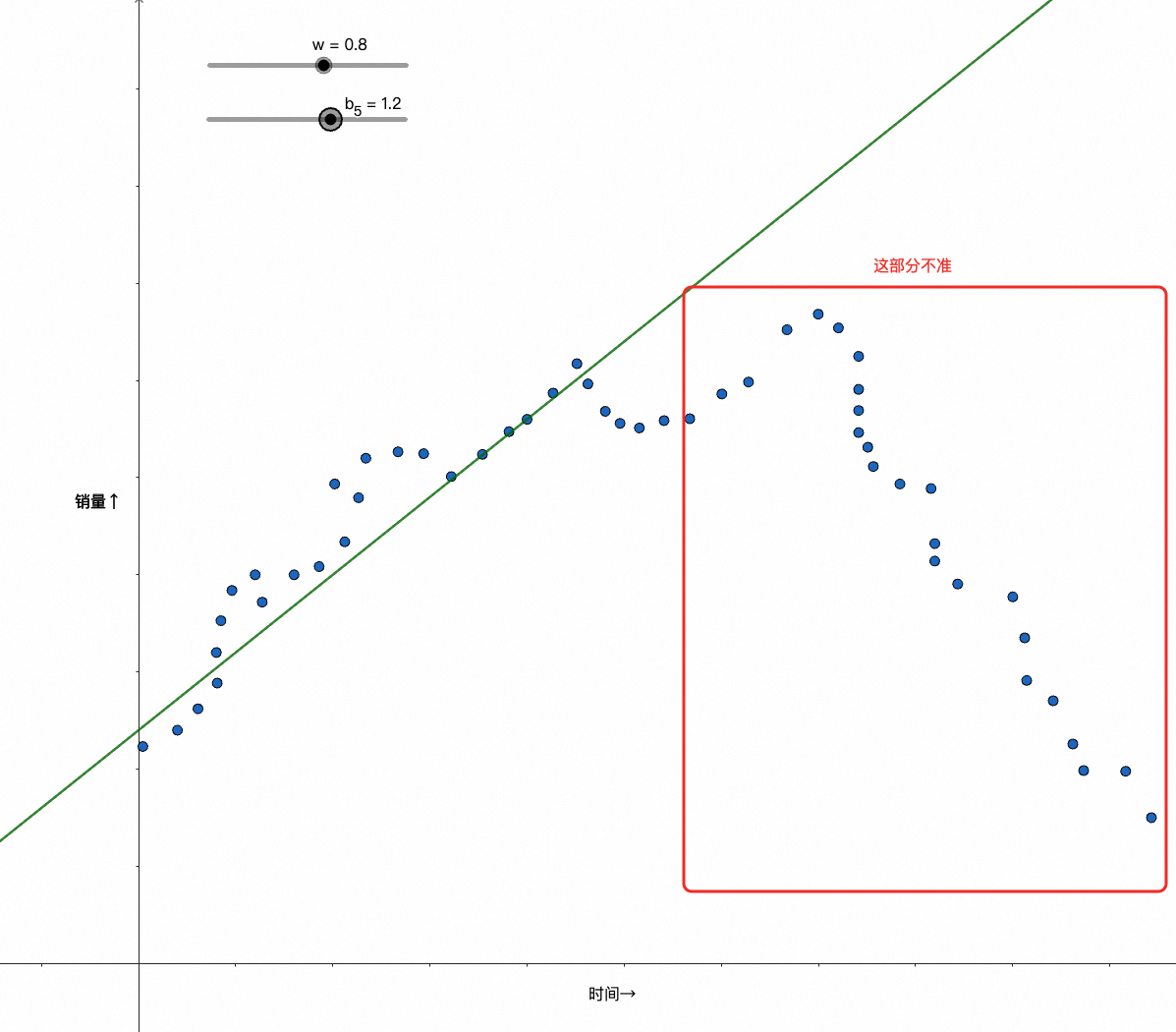
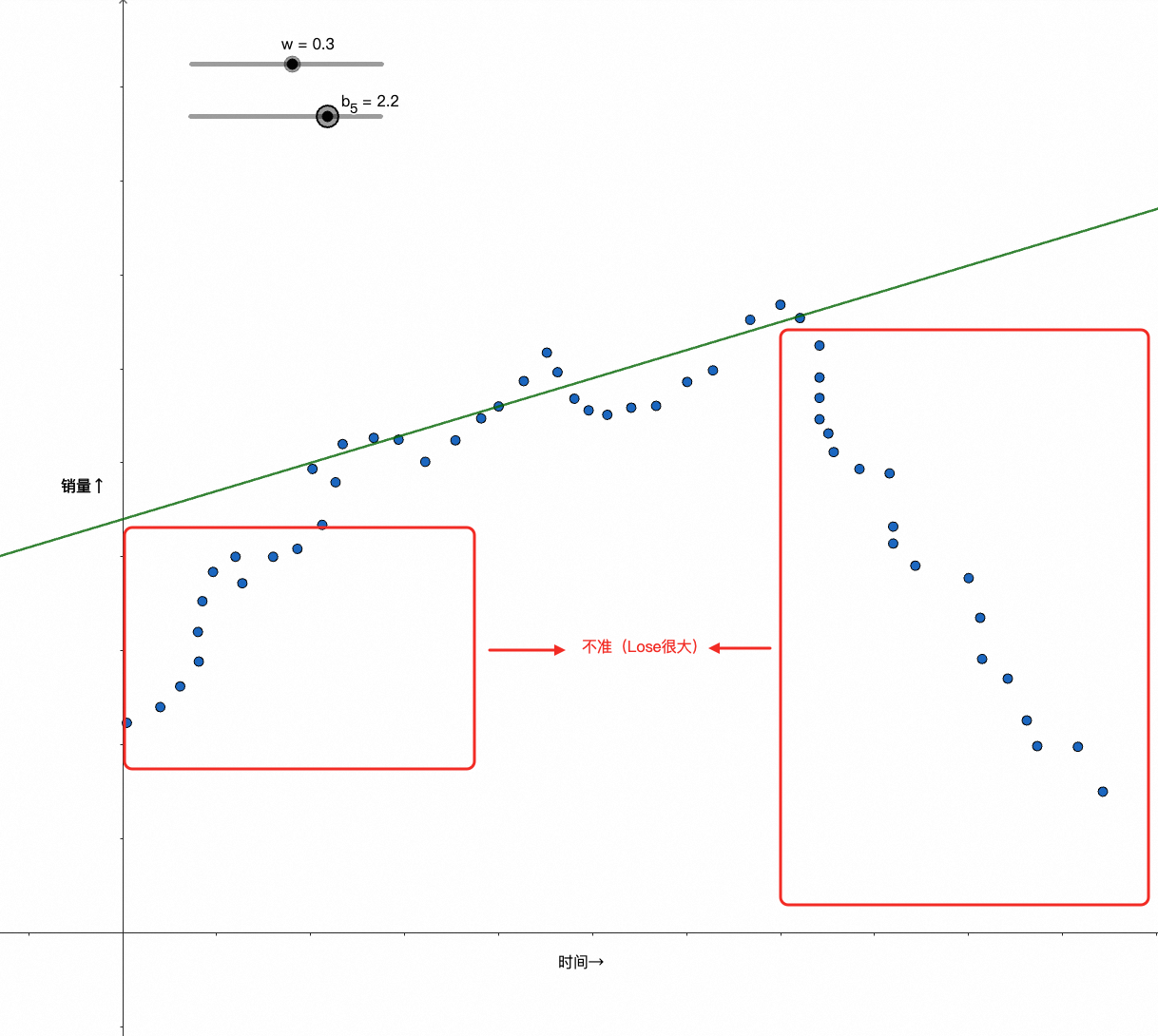
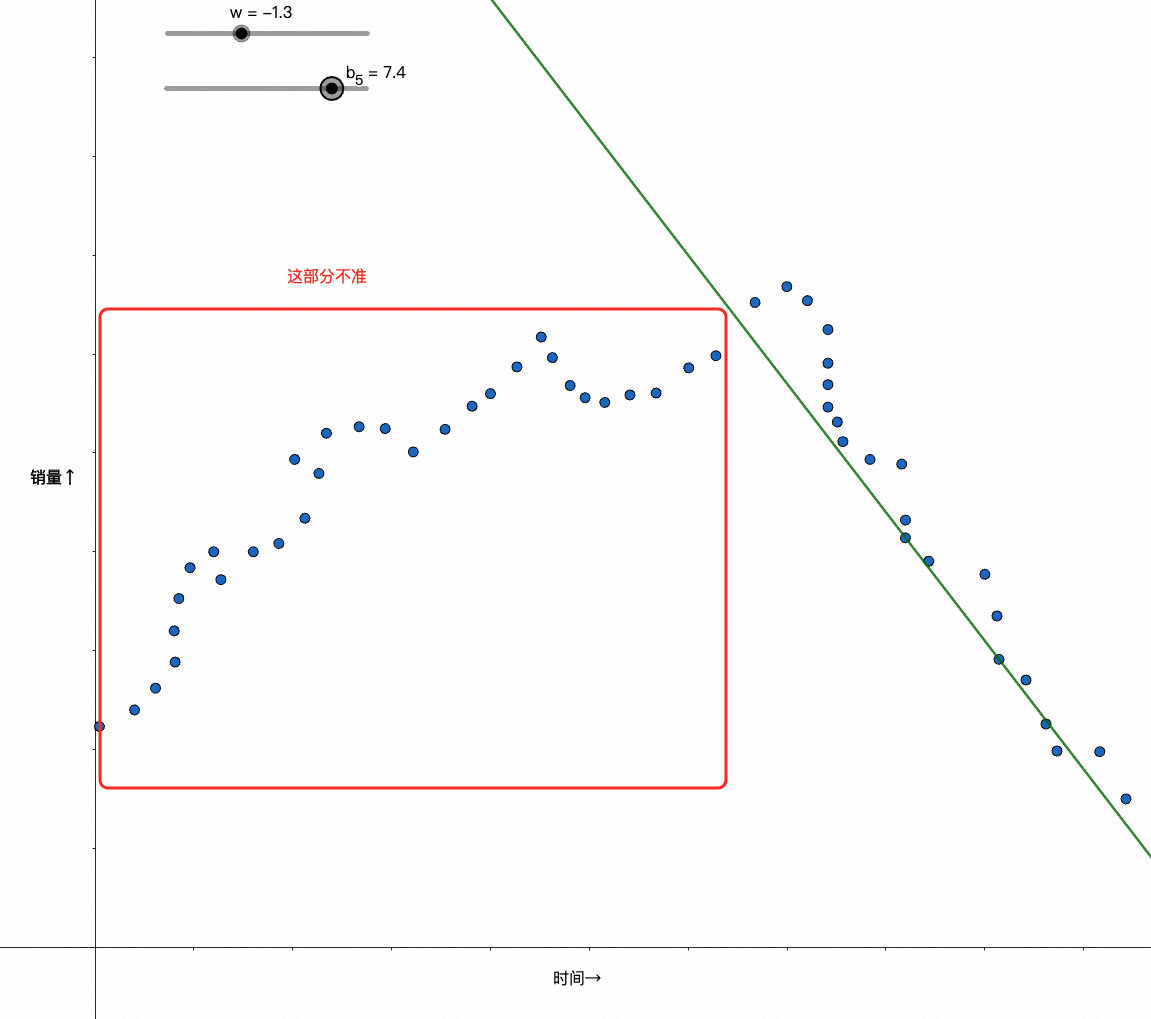
到这里你可能会想起微分课上学过的泰勒展开，知道解法；也可能，你考完试后就再也没有用过相关知识，并且工作多年已经忘得差不多了
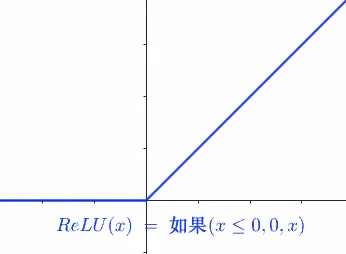
但在这里，我并不打算复习/深入讲解这部分内容，所以即便是后者也没有关系，你只需要知道利用激活函数，可以做到类似的非线性变化，比如引入ReLU并拆成多组w、b，就可以更好的拟合数据了，ReLU原始函数图像如下所示：
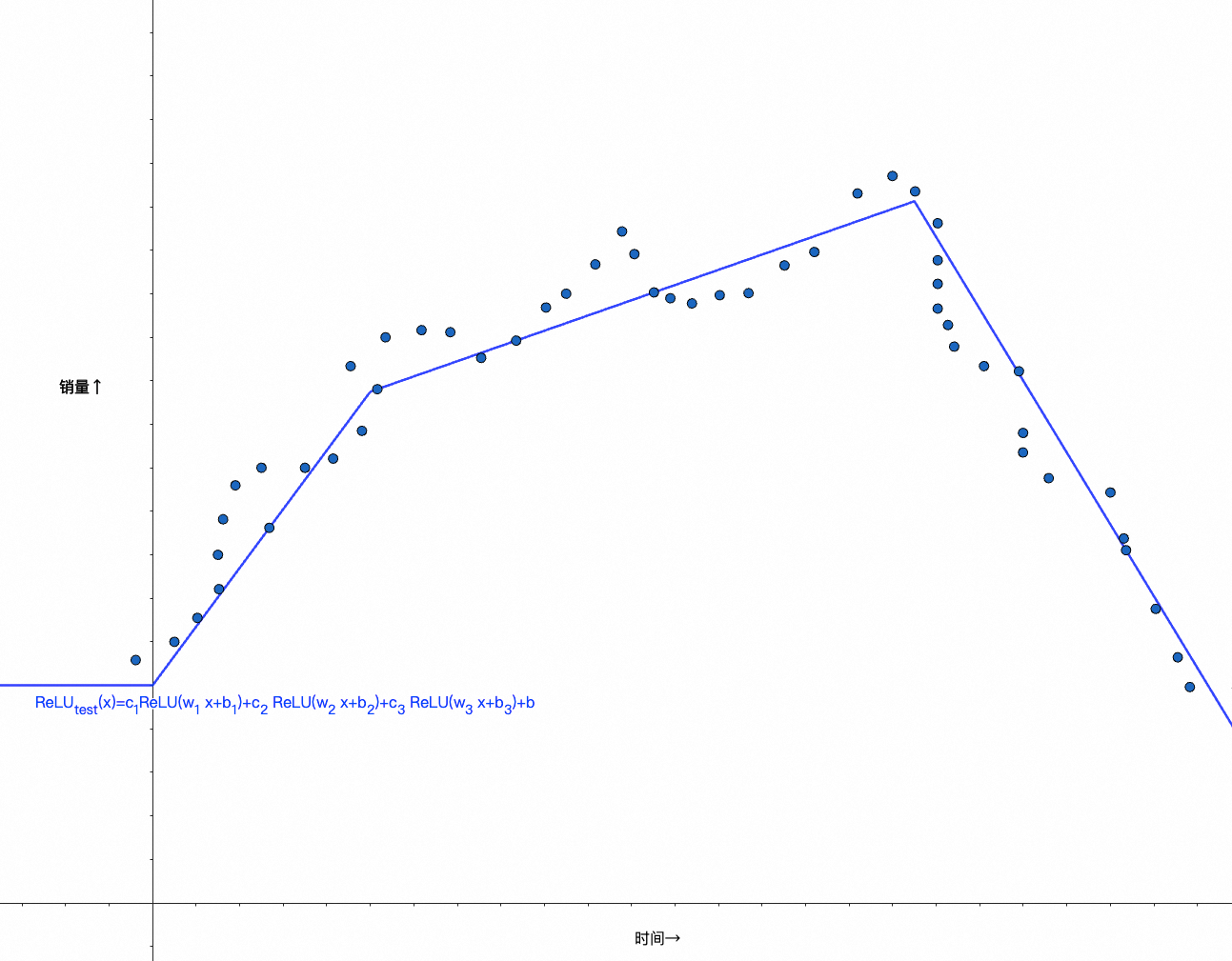
经过三组w、b组合，可以得出如下函数，逼近测试数据：
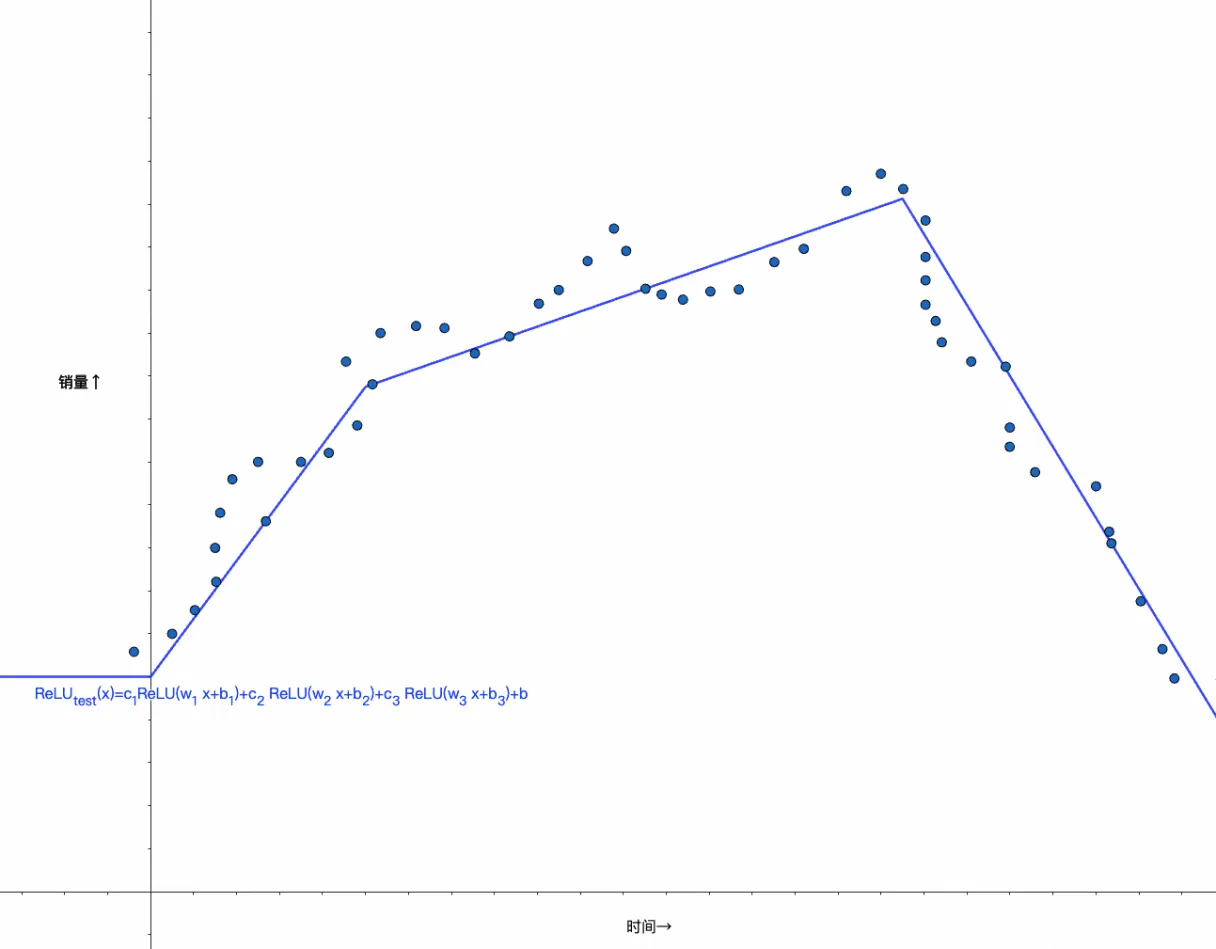
- - $c_{1} ReLU(w_{1} x+b_{1})+c_{2} ReLU(w_{2} x+b_{2})+c_{3} ReLU(w_{3} x+b_{3})+b$
你可以再尝试下用线性函数，是得不到上面结果的，它永远是一条直线：
如果你还没悟到上面的线段是怎么变出来的，那我们可以把过程再拆分下：
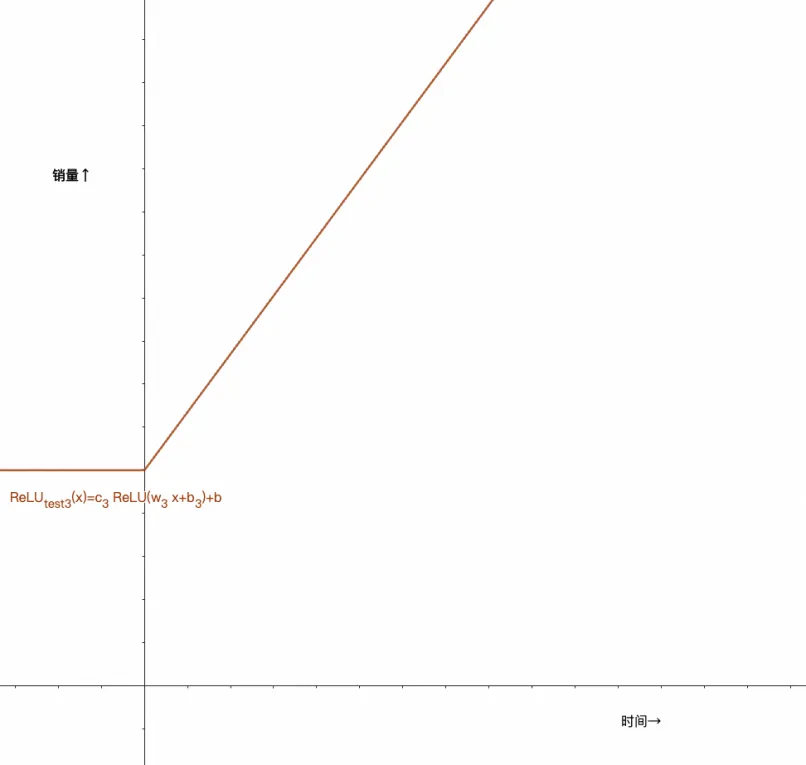
- 这是 $c_{3} ReLU(w_{3} x+b_{3})+b$ 的函数图像（ $+b$ 的作用是把函数图像向↑平移了一段）：
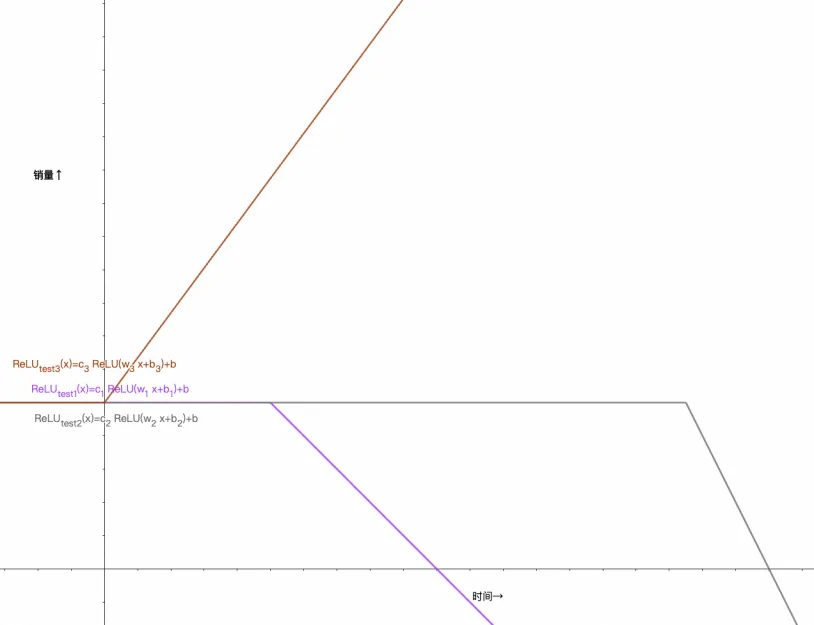
- 再把 $c_{2} ReLU(w_{2} x+b_{2})+b$ 显示出来：
- 再把 $c_{1} ReLU(w_{1} x+b_{1})+b$ 显示出来：
- 最终与我们一开始拟合出的函数对比，不难看出，这其实就是将三个ReLU分段函数的结果相加：
- 眼尖的人可能会注意到上面除了w、b外还多了个c，这个参数好像没见过呀，但其实这个c之后也会转化成w，下面「向量/矩阵化」就会讲到

神经元与神经网络

⚠️ 如果你是直接跳到这里的，建议马上掉头，把上面的东西一字不漏的看完🤣

其实有关神经元和神经网络的内容我上面已经讲完了，只不过表达方式稍有不同，所以下面我会对上面的内容进行一些"转换"，让你彻底明白
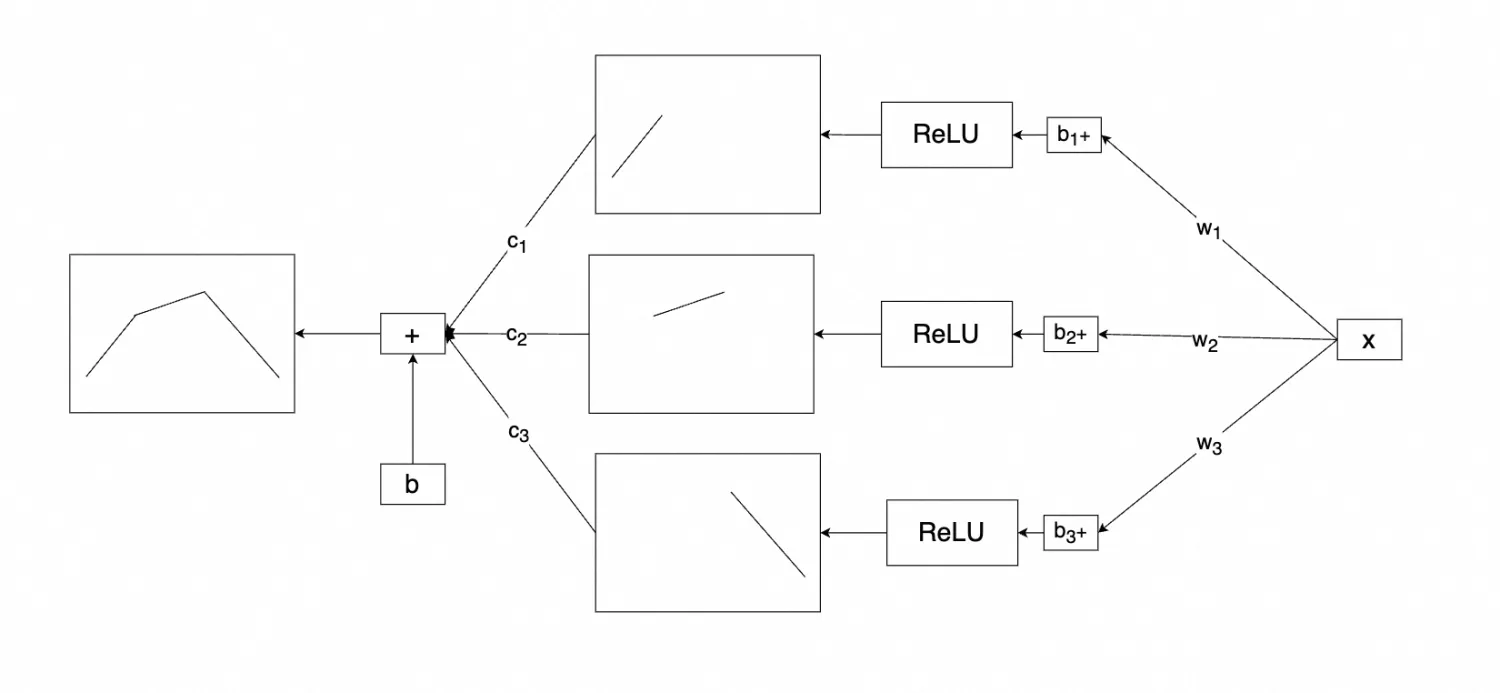
上一个非线性case中，我们提到一个复杂的函数是可以通过很多分段函数组合而成的，因此对于这个行为，我们可以画成如下图理解：
我再把图变一下，神经网络就"出现"了，包含神经元、隐藏层、输出等：
- 平时见的很多圆圈连在一起，也是这么来的，只不过他们的神经元、隐藏层等数量更多
- 需要注意的是：神经网络不一定需要激活函数，比如前面的case中，即便没有激活函数也可以进行梯度下降
不难看出，神经网络就是一个可以不断通过梯度下降、反向传播更新参数，从而拟合实际数据的预测函数。
如果隐藏层有多层，就长下面这个样子：
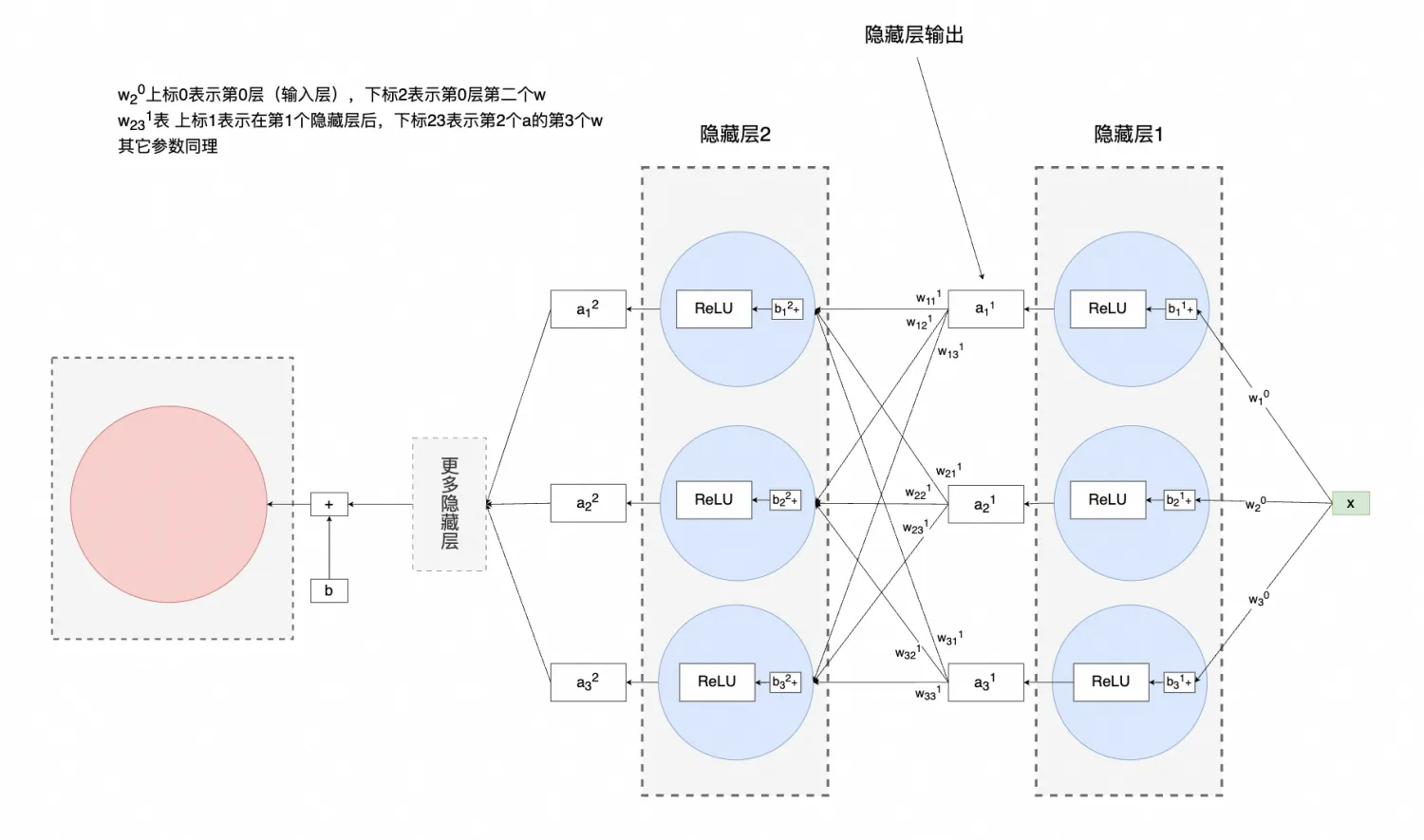
- 当然，最终输出也可以有多个（分类问题），这里就不再展开
- 这种结构通常也叫全神经网络

小扩展

向量/矩阵化

🌱 通常，实际使用训练框架时，往往使用的是张量（Tensor）来表示多维数据，比如"向量"是就是一维张量，"矩阵"是二维张量，当然还有三维、四维等更高维度的张量；因为我之后主要是从几何意义的角度，所以还是使用向量、矩阵声明，读者只要知道还有这么个东西即可，无需过分纠结

上面的case中，我们只设定一个x来预测（相当于一个维度），这个x可以是人气值，可以是时间，也可以是优惠金额等等
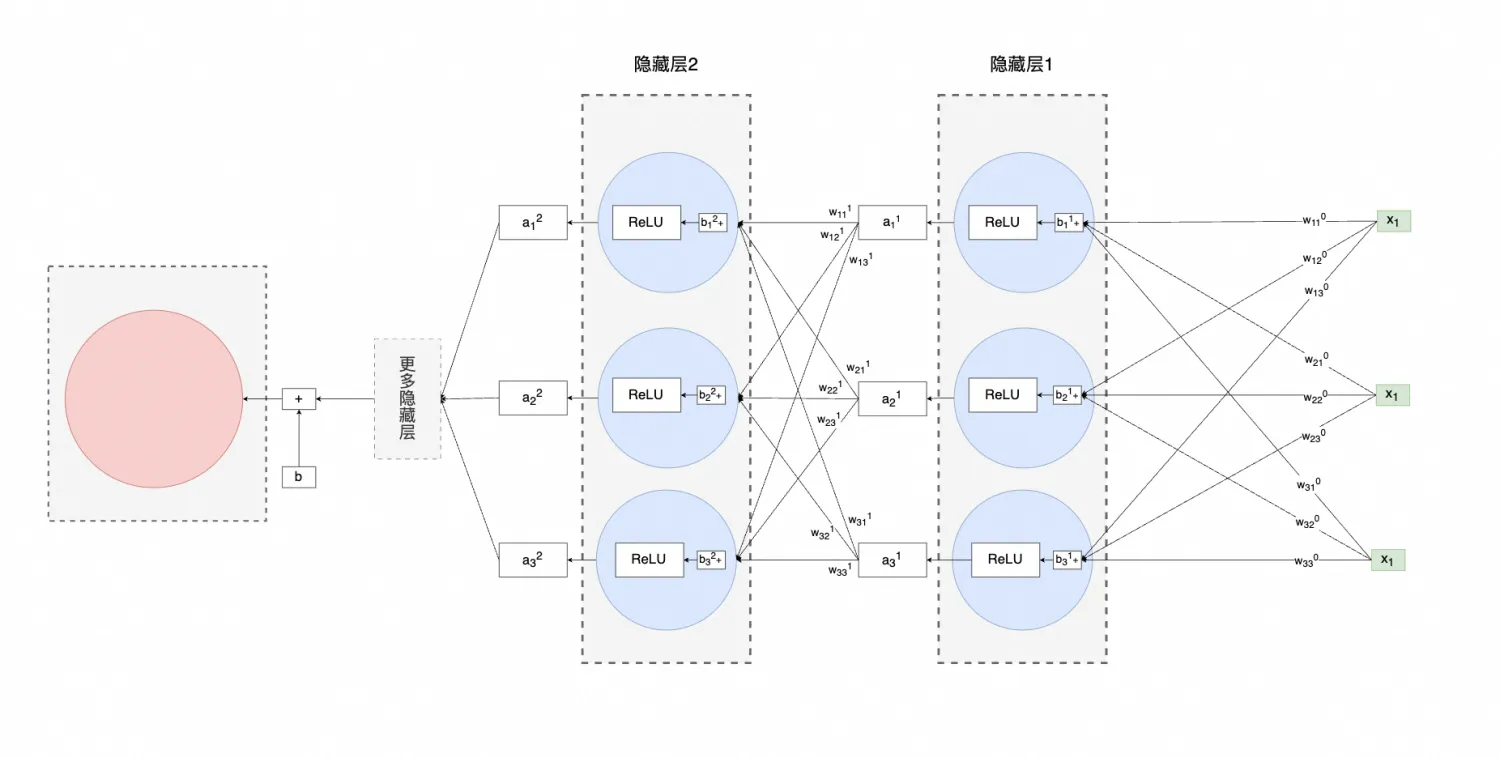
但往往实际训练时，会同时使用多个维度，比如 $x_1$ 是人气、 $x_2$ 是时间、 $x_3$ 是价格等等，神经网络就会变成下面这样：
把上图到隐藏层1输出为止的内容写成计算式，大概就是下面这样：
$a_1^1 = w_{11}^0 x_1 + w_{12}^0 x_1 + w_{13}^0 x_1 + b_1^1 \\[1em] a_2^1 = w_{21}^0 x_2 + w_{22}^0 x_2 + w_{23}^0 x_2 + b_2^1 \\[1em] a_3^1 = w_{31}^0 x_3 + w_{32}^0 x_3 + w_{33}^0 x_3 + b_3^1$

进一步，可以用矩阵乘法表示，则如下所示（行乘以列）：

\begin{bmatrix} a_1^1 \\[1em] a_2^1 \\[1em] a_3^1 \\ \end{bmatrix} = \begin{bmatrix} w_{11}^0 & w_{12}^0 & w_{13}^0 \\[1em] w_{21}^0 & w_{22}^0 & w_{23}^0 \\[1em] w_{31}^0 & w_{32}^0 & w_{33}^0 \\ \end{bmatrix} \begin{bmatrix} x_1 \\[1em] x_2 \\[1em] x_3 \\ \end{bmatrix} + \begin{bmatrix} b_1^1 \\[1em] b_2^1 \\[1em] b_3^1 \\ \end{bmatrix}

当然，如果你知道一部分渲染知识 / 看过一些代码 / 看过其它一些解释，可能会指出矩阵不是从右向左乘吗？我的回答是，暂时忽略这些细节= =

再进一步简化（暂且用'表示这个一个向量/矩阵）：

a_{1}'=w_{0}'x' + b_{1}'

再把激活函数加上去：

a_{1}'=ReLU(w_{0}'x' + b_{1}')

如果把第二层输出也套娃进来，你就明白前面提到的 $c_1$ 、 $c_2$ 、 $c_3$ 本质也是w：

a_{2}' = ReLU(w_{1}' \: \cancel{\bcancel{c_{1}'}} \: ReLU(a_{1}'=ReLU(w_{0}'x' + b_{1}')) + b_{2}') \\[1em]

其实就是下面两个式子套娃：

a_{2}'= ReLU(w_{1}' a_{1}'+b_{2}')\\[1em] a_{1}'=ReLU(w_{0}'x' + b_{1}')

如果你觉得上面的内容有点不明所以，也不打紧，因为上面讲向量/矩阵化的意义是为了后续遇到Transformer矩阵时，不会过渡得太突兀，留个印象便可，后续讲到几何意义的时候会更清楚

如何理解提升维度能解更多问题

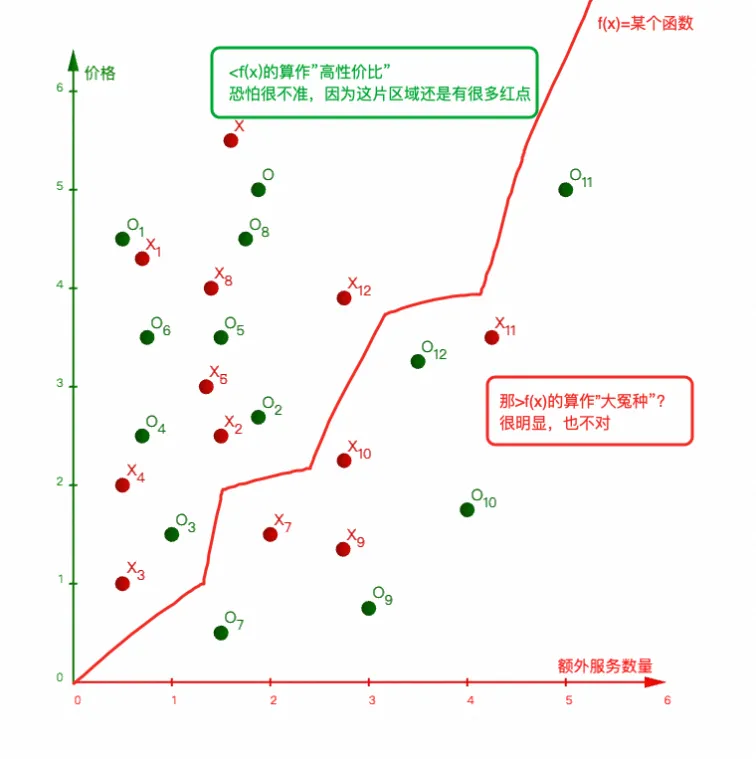
假设现在是要通过酒店的价格、服务数量，来做一个分类，分出"高性价比酒店"和"大冤种酒店"
按照实际数据把函数图画出来可能是下面这样（红色是"大冤种"，绿色是"高性价比"）：
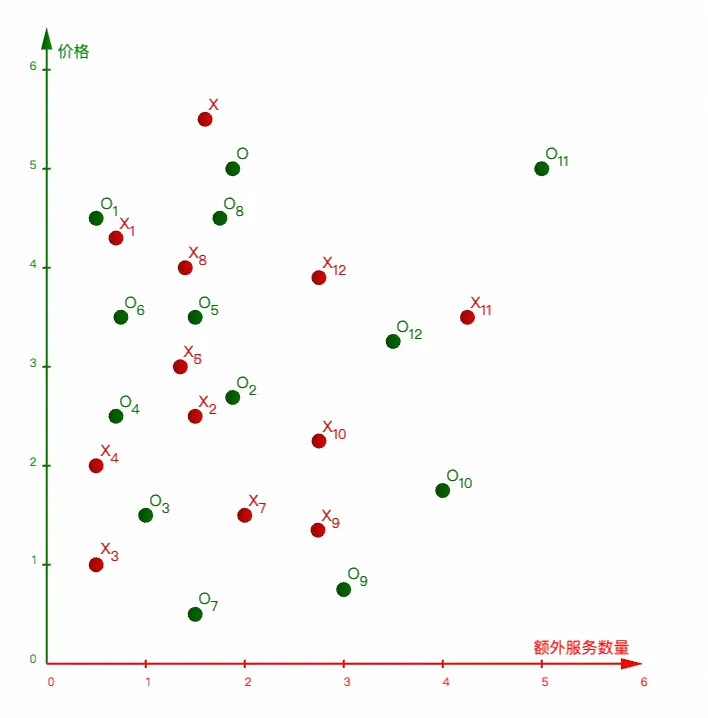
- 这个case应该是挺符合直觉，服务量多并不意味着服务质量高，量大低质量还是觉得亏
上面的分布可以看做是几乎无法分类，尤其是数据集继续膨胀的情况：
但，真的就无解吗？或许你可以实现一个处处可导且能分类上述问题的新神经网络，不过成本可能非常高；实际上有更好的办法解决，那就是增加数据的维度
比如，这里增加新的维度：好评率，就会发现这个问题变得非常简单：
所以，这里想让你明白的是：通过增加维度来训练找问题解，往往能超越你眼睛所看到的"路"，比如ChatGPT-3一个Token就有12288个维度，后续模型只高不低= =

Transformer

矩阵基础

不知道你在打游戏，比如黑悟空的时候，有没有想过这样一些问题：
- 金箍棒能长变短，在程序中是怎么实现的？
- 答：缩放矩阵
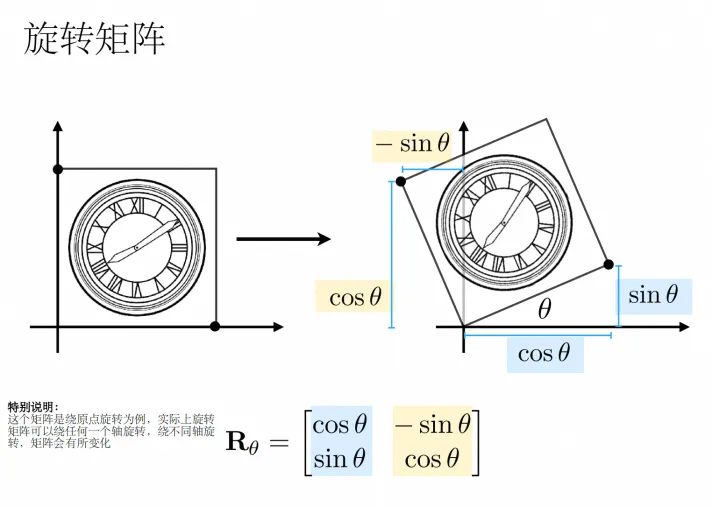
- 悟空能在空中360°的旋转，是怎么做到的？
- 答：旋转矩阵
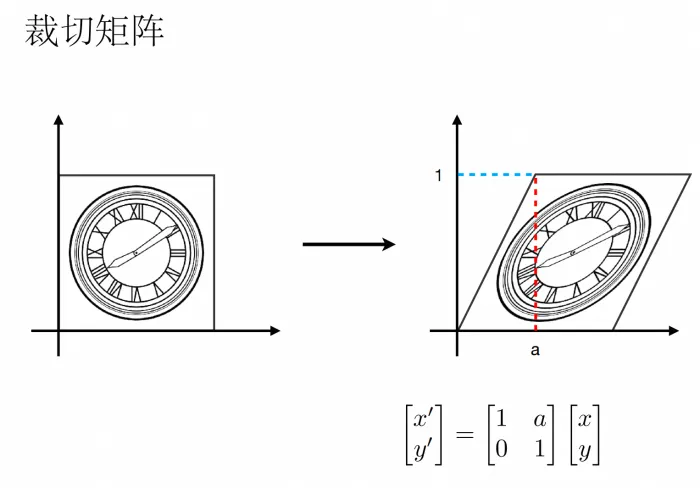
- 有时候看起来个弹簧一样，duang的弯曲了，是怎么做到的？
- 答：可能是裁切矩阵
- 那3D的场景是如何在2D屏幕中显示的？答：投影矩阵（降维）
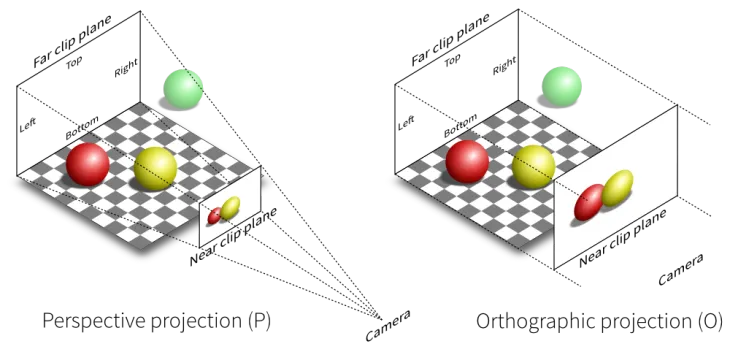
  - PS：把XXX"投影"通常就表示降维

总之，这里的目的不是为了推一遍矩阵的公式，这一小节的目的是为了让你有如下一种直觉：
- 无论是一个点/向量/矩阵，当它与另一个矩阵相乘时，你都可以当做它对空间进行了"扭曲"，这个扭曲造成的结果可能导致向量变长变短（缩放）/方向变化（旋转）等，也有可能把向量映射到更高维升维↑/更低维（降维↓）的空间

向量基础

这里涉及到的向量基础只有两个：向量相加、向量点积，这里只要了解它们的几何意义即可
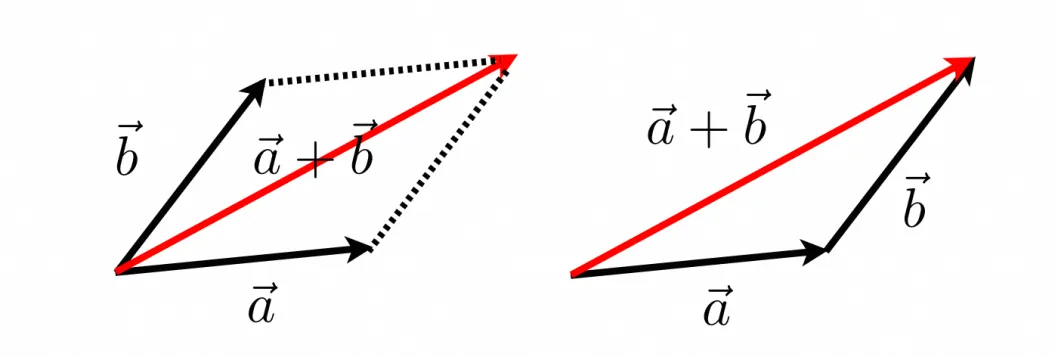
先说向量相加，相信学过勾股定理不难理解：

至于向量点积，可以理解为：两个向量越靠近（夹角越小），点积结果就越大
比如下面的动画就是两个单位向量（长度=1的向量），从180°到0°的过程：
这里我也不卖关子了，之所以提到上面两个基础，是因为它们跟Transformer的实现密切相关，这里建议留下强印象，或者之后讲到相关内容时忘记了的时候记得翻回来

Embedding的由来

这里我们先说一个非常符合直觉的事情：如果要让机器理解说话，首先需要将一句话进行分词、数字化表示
先说分词，比如「我要买一斤苹果」可能会被拆分成「我」「要」「买」「一斤」「苹果」，这里每一个被「」包裹的词，也称作token
之后，为了让计算机知道token和token之间的联系，你需要将不同的token数字化才行，这时你可能会尝试对每一个token转成唯一id，然后把id投影到一个一维坐标系上，用坐标之间的距离表示token之间的联系，比如：
嗯～看起来似乎可以，苹果葡萄表示水果这个物种，确实得离得近一些，但如果这个苹果指的是手机呢？：
这时候，问题就变成：明明两个都是手机，应该靠得更近才对，但因为前面已经用来跟表示水果这一维度的距离，所以无法再表示手机了

好，现在问题变成了维度不够了，那我就把维度发挥到极致，把每个token都当做是一个独立的维度
比如苹果=[1,0,0]、华为=[0,1,0]、葡萄=[0,0,1]，画成3D图则如下所示：
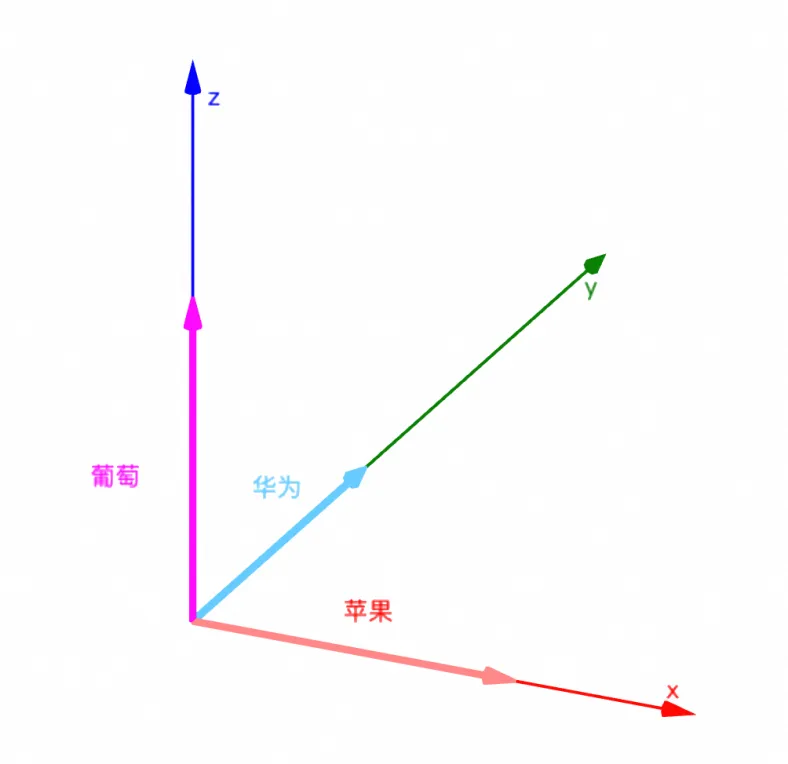
- 实际上，这种方式有个专属术语，那就是one-hot，one-hot的大小=词汇表的大小，无用0占的空间非常大
但很遗憾，one-hot做得太极致了，虽然维度提升了，但却丢失了"距离"的表示，每个token之间都是互相垂直，无法体验语义关系

那有没有一种方式，可以即表示token与token之间的联系，又兼容多个维度的语义呢？
有的，兄弟，有的，那就是把token转成向量，再计算向量点积来表示"距离"
而Embedding(嵌入)就是通过嵌入矩阵把先前的one-hot投影（降维）成另一个空间的向量：
当一个token被转成向量后，这个向量的每个维度可能都会表示一层语义，比如像下面这样：
总之，到目前为止，生成了两个东西：
- token转成的id（每个token与id都是映射关系）
- token转成的向量
那前面提到的one-hot呢？其实并没有生成，毕竟真生成出来的话空间非常大，一种优化的做法是直接通过token转成的id索引Embedding矩阵中的对应行，以此来跳过了生成one-hot的步骤
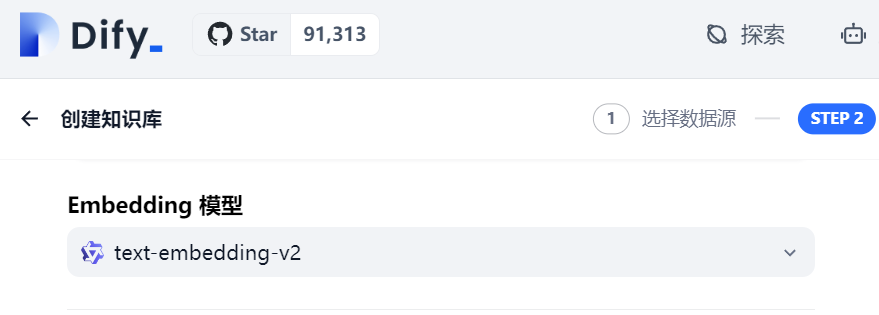
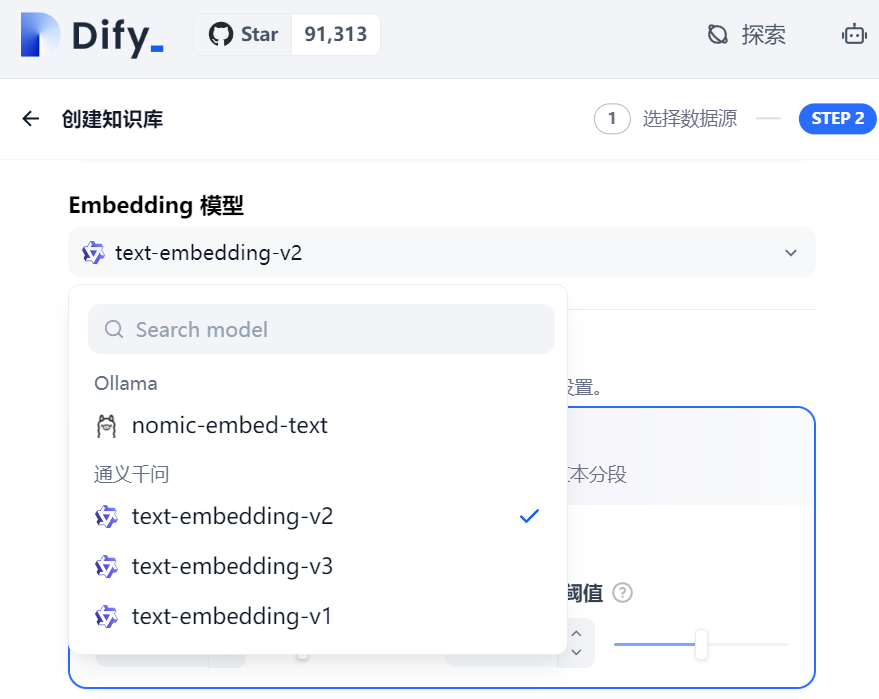
或许你在跟大模型对话的时候不知道有Embedding的存在，但相信当你使用到知识库/RAG等能力时，很快就会遇上的，比如Dify的知识库设置：
实际上，Embedding中将token转为向量的嵌入矩阵也是训练出来的，只是说"降维"可能不太准确，"降维"只是副产品，整个过程的主要目是获得语义信息丰富的稠密向量
至于怎么训练就不在本文范围了，感兴趣的下来自己了解下= =

嵌入空间 & 在这之后

在「矩阵基础」部分，我们了解到跟矩阵做乘法时，实际上可以理解为对空间产生了"扭曲"
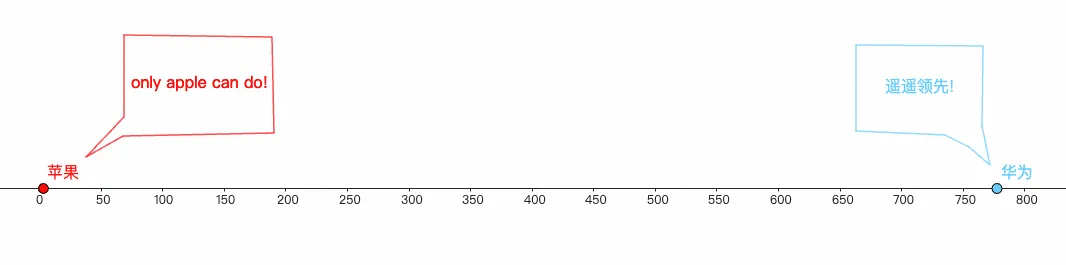
而token经过嵌入矩阵转为向量后，实际上可以看做：这个token被转换成了嵌入空间中的一个向量
在这个空间中，每个向量之间都可以计算点积，通常点积结果越大说明关联性越强，比如：

鸡 \cdot 白切鸡 = 0.7 \\[1em] 鸡 \cdot 走地鸡 = 0.66

如果你的嵌入矩阵喂的全是小黑子的资料，那么可能会出现：

鸡 \cdot ikun = 0.99

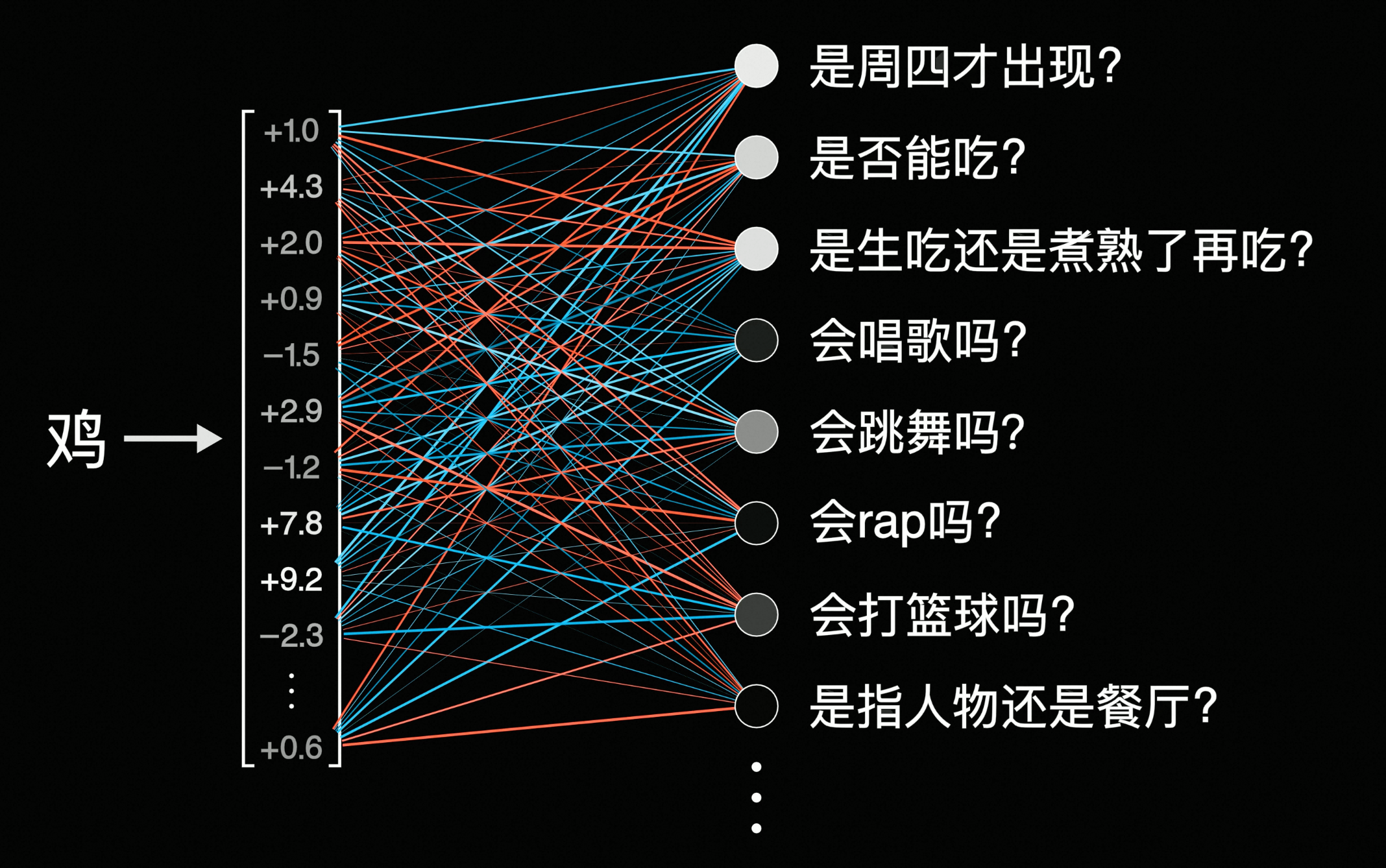
除此之外，鸡这个向量还可能表示很多别的含义，如果将各地鸡相关的菜谱和小黑子资料投入到训练当中，那么训练后的嵌入矩阵，可能会将相关token转换成如下向量：
在嵌入空间中，一个鸡能表示N多个含义，但我们说话的时候，通常只会显示地表示一个含义，比如，如果上一句话提到"疯狂星期四"，那么后面说"吃鸡"中"鸡"的含义大概率是指"肯德基"，而不会指"ikun"、"白切鸡"等含义。
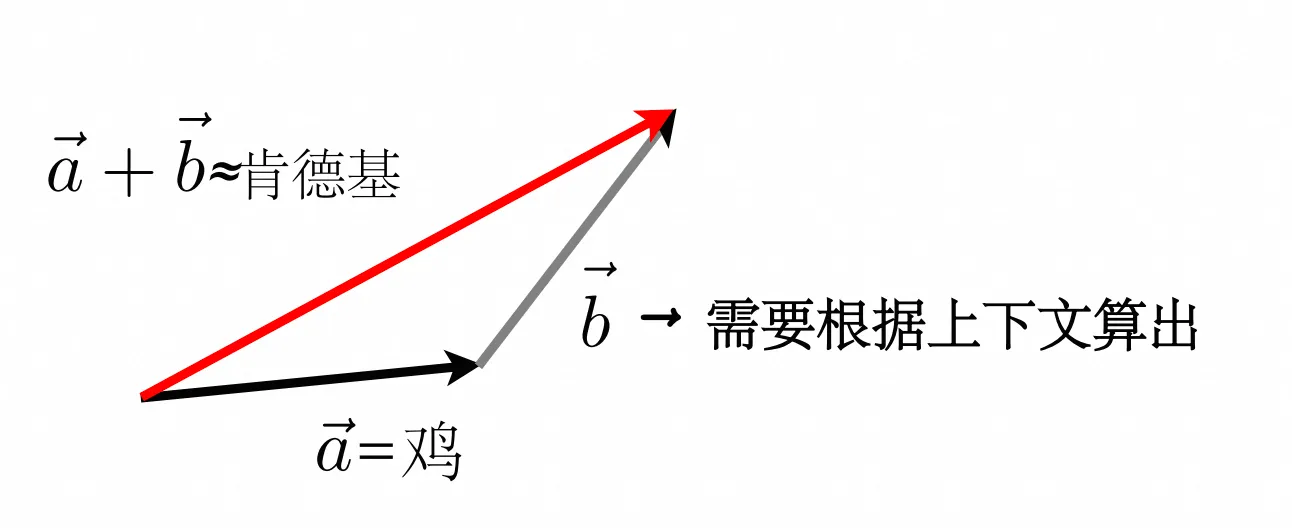
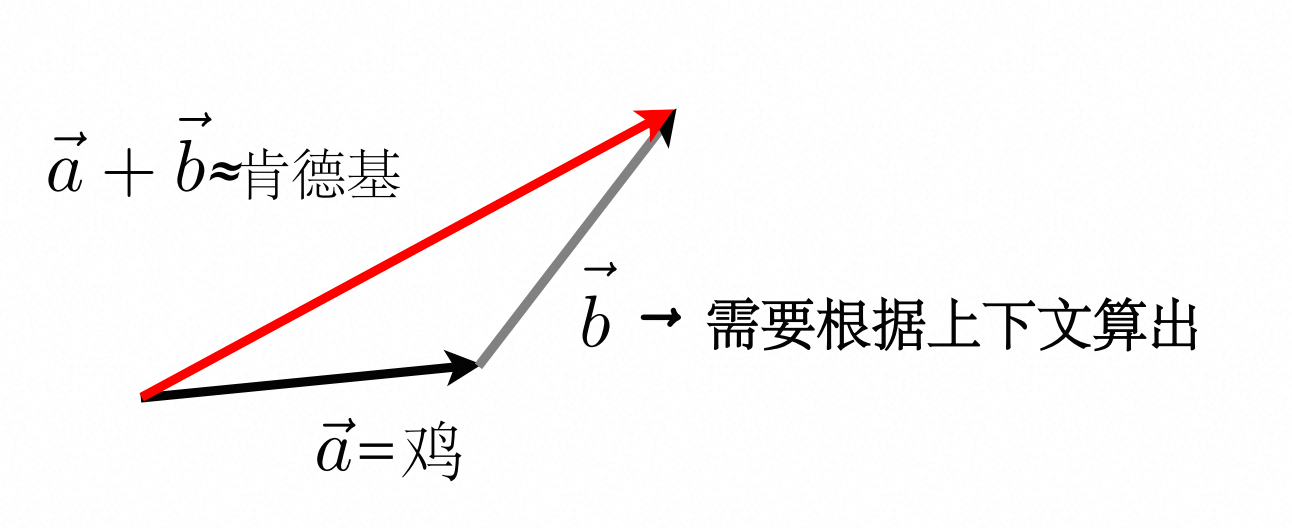
还记得「向量基础」中提到加法吗，后续步骤中，我们就是要根据上下文信息算出灰色那条向量 $\vec{b}$ ，让「鸡」向量与其相加，变成「肯德基」：
所以到这里，我希望你明白的是：Embedding结束后，只是完成了最基础的语义关联，此时一个向量的任何一个维度都可以表示一重语义，而「如果上一句话提到"疯狂星期四"，那么后面说"吃鸡"中"鸡"的含义就是指"肯德基"」这个根据上下文决定最终表示哪个语义的步骤，则是在这之后的自注意力+FNN等模块解决的事

当然，这里的「最基础的语义关联」听起来有点鸡肋，还记的上个小节提到「整个过程的主要目是获得语义信息丰富的稠密向量」吗，实际上它里面有很多东西是可"复用"的，最经典的例子就是： $\vec{女王} \approx \vec{国王}+\vec{女}-\vec{男}$
类似的还有「姐姐-弟弟」「单数-复数」等等

Transformer结构预览

再了解Transformer的架构和其中细节之前，我想先让你知道：LLM的文本生成，本质上是不断地预测下一个Token，比如像下面这段动画一样：
- 这种方式也被称作自回归生成
- 之所以现在提起这个概念，是希望让你继续往下看时，知道最终目标就是要预测，而需要重点关注的是：它是如何预测的？
- PS：实际Transformer可能不是直接选择概率最大的词，而是会用束搜索等策略选择"全局最优"的路线，这里使用贪心搜索还是为了方便直观地理解
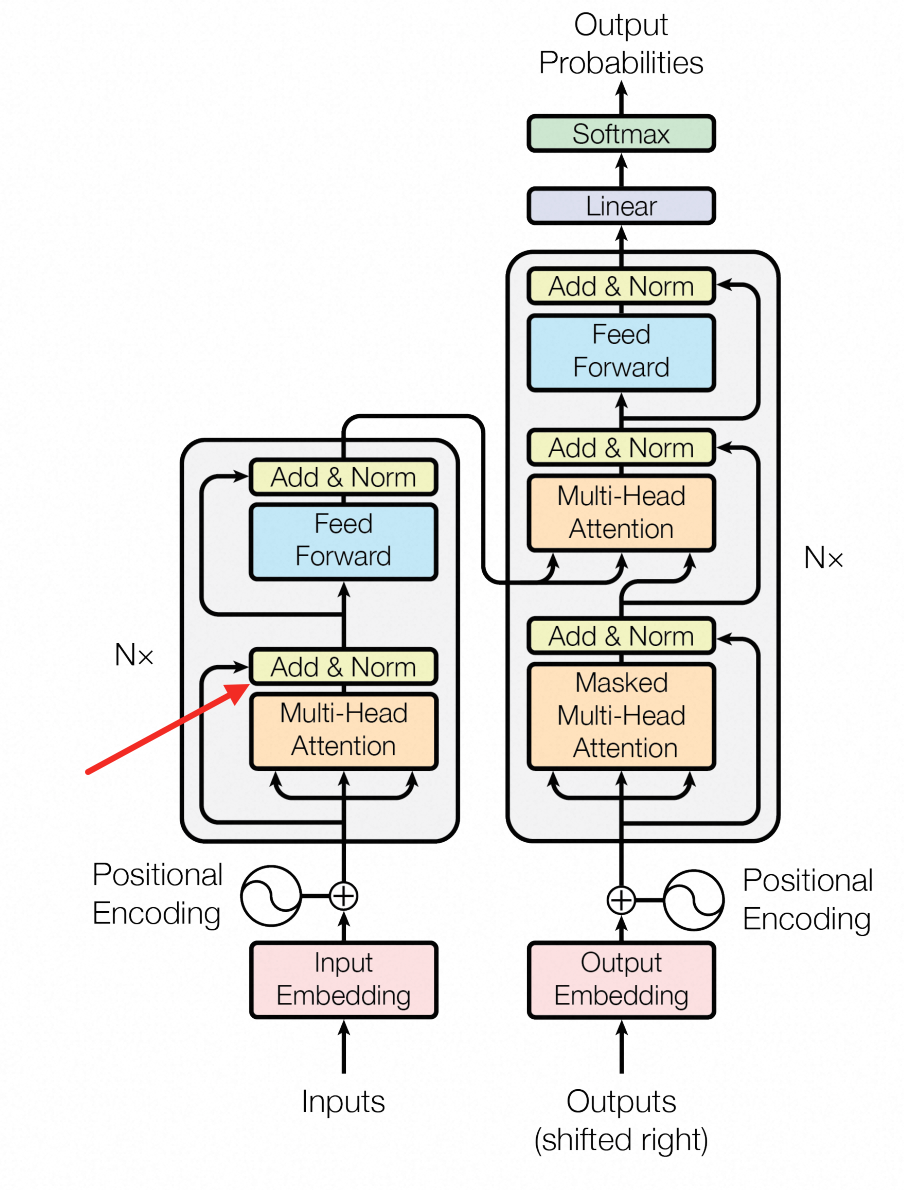
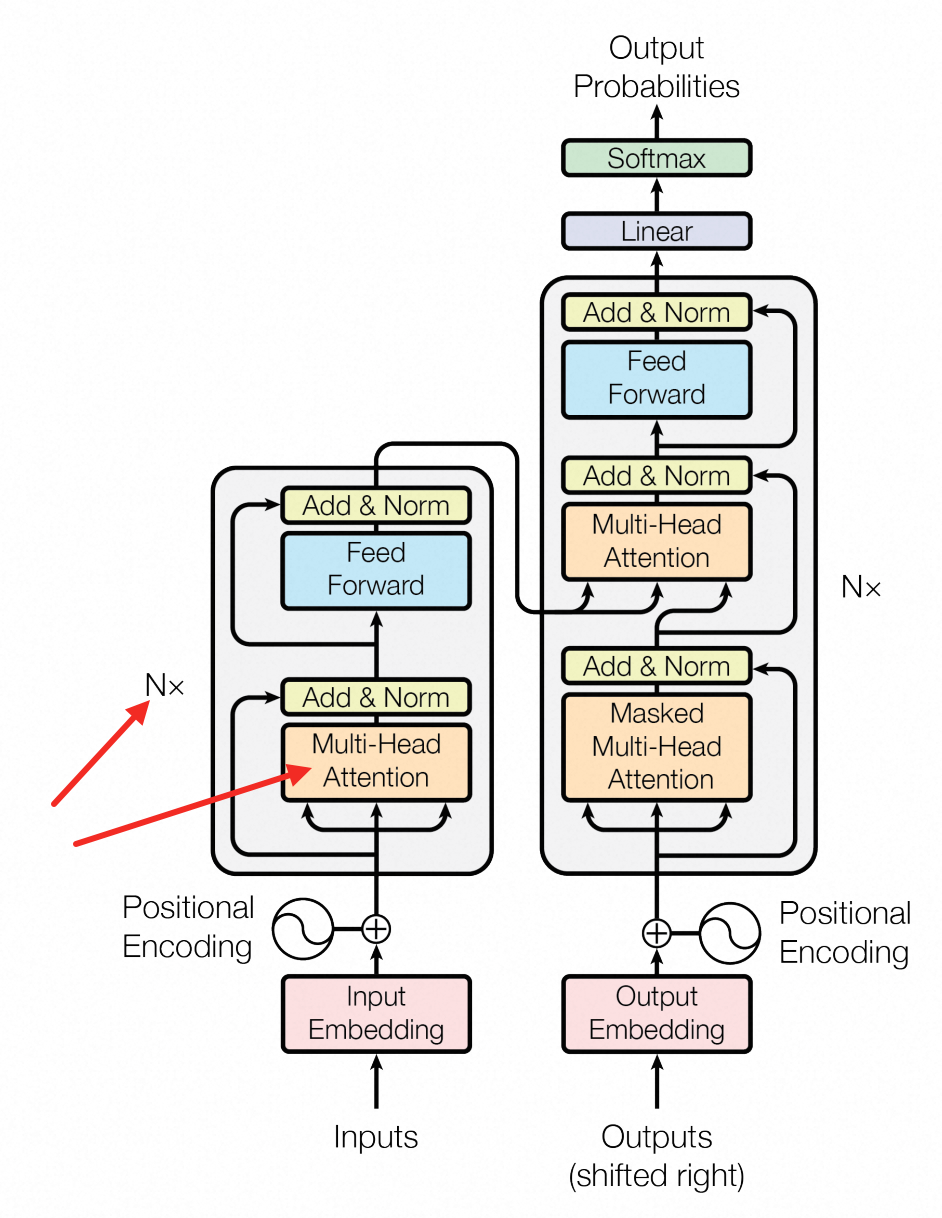
下面先来看下Transformer论文中，整体架构的模型图（顺便翻译一下）：
Embedding上面已经聊过了，相信你已经了解得比较清楚了
位置信息这里就简单提一嘴，它的作用是告诉模型语句的时序信息，因为计算过程是并行的
剩下的东西里面，最最最核心的其实就是注意力机制了，了解清楚这东西，别的的都好说，所以接下来就先讲清楚什么是自注意力机制

自注意力机制（self-attention）

这里第一次提到QKV矩阵你可能会比较懵逼，但还是建议继续读下去，在下一小节有一个很通俗的解释，看完后再重新理解这一节的内容会变得简单很多

上文中提到「根据上下文决定最终表示哪个语义的步骤，则是在这之后的自注意力+FNN等模块解决的事」
所以现在第一个问题就是，如何关联上下文呢？上面铺垫了这么多，相信你不难猜到，还是点积
只不过不是直接拿Embedding后的向量 $\vec{E}$ 直接跟上下文点积，而是让向量经过 $W_Q、W_K、W_V$ 矩阵得到新的向量 $\vec{Q}、\vec{K}、\vec{V}$ 再点积，由于 $\vec{V}$ 要结合残差连接才能看出作用，我们这里先忽略它，只看 $\vec{Q}、\vec{K}$ ，转化成点积的过程如下所示：
但如果你这时去瞄一眼Transformer的论文，会发现它的公式好像和点积没什么关系：

Attention(Q,K,V) = softmax(\frac{QK^{T}}{\sqrt{d_k}})V

但实际上，这只是在用矩阵的方式表示，把它转换一下，你会发现本质上还是点积：
- $K^T$ 表示转置矩阵，就是行列互换的意思
- $\sqrt{d_k}$ 在这里不需要太关注，原文中说是用来避免梯度消失等问题
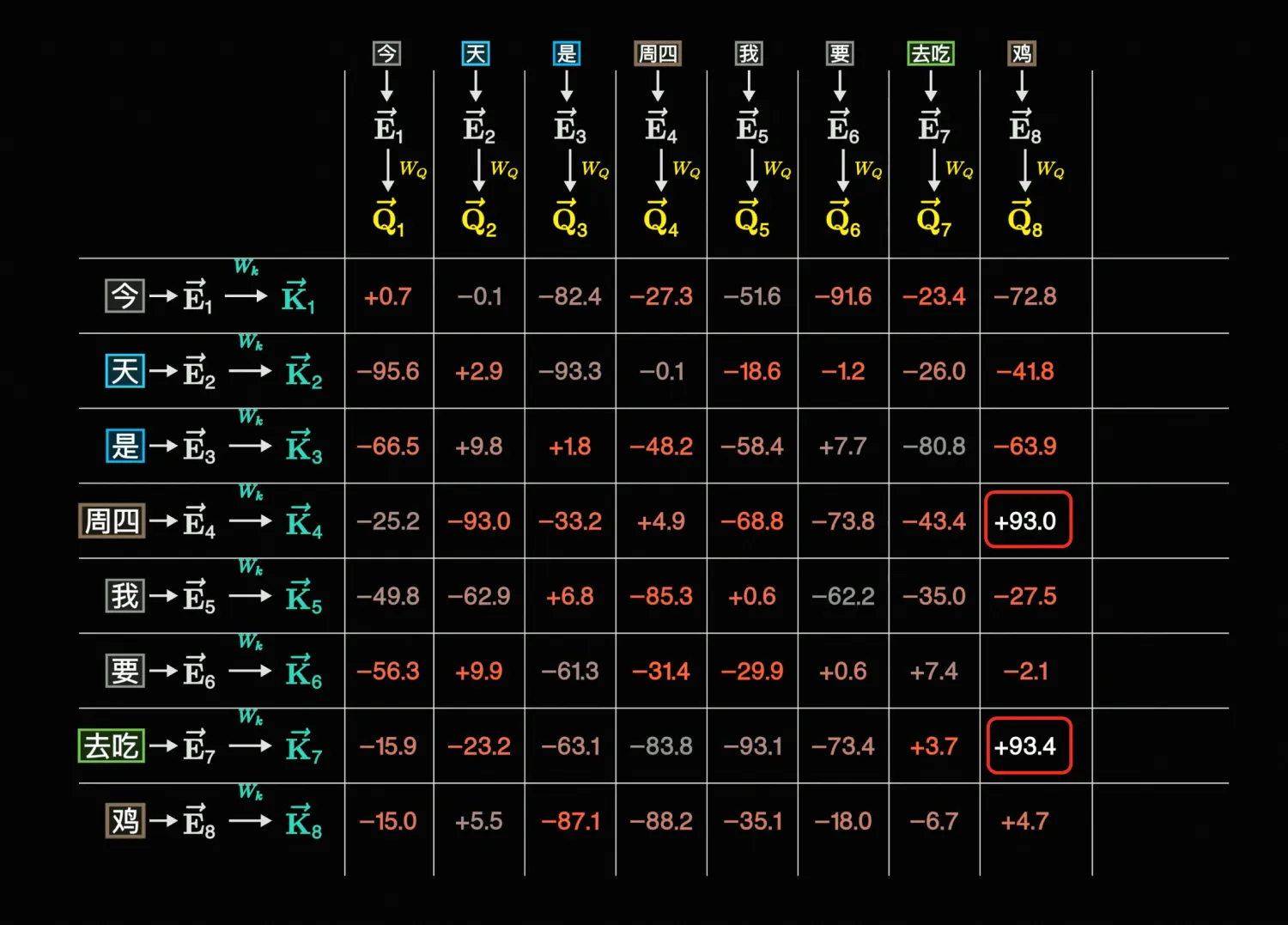
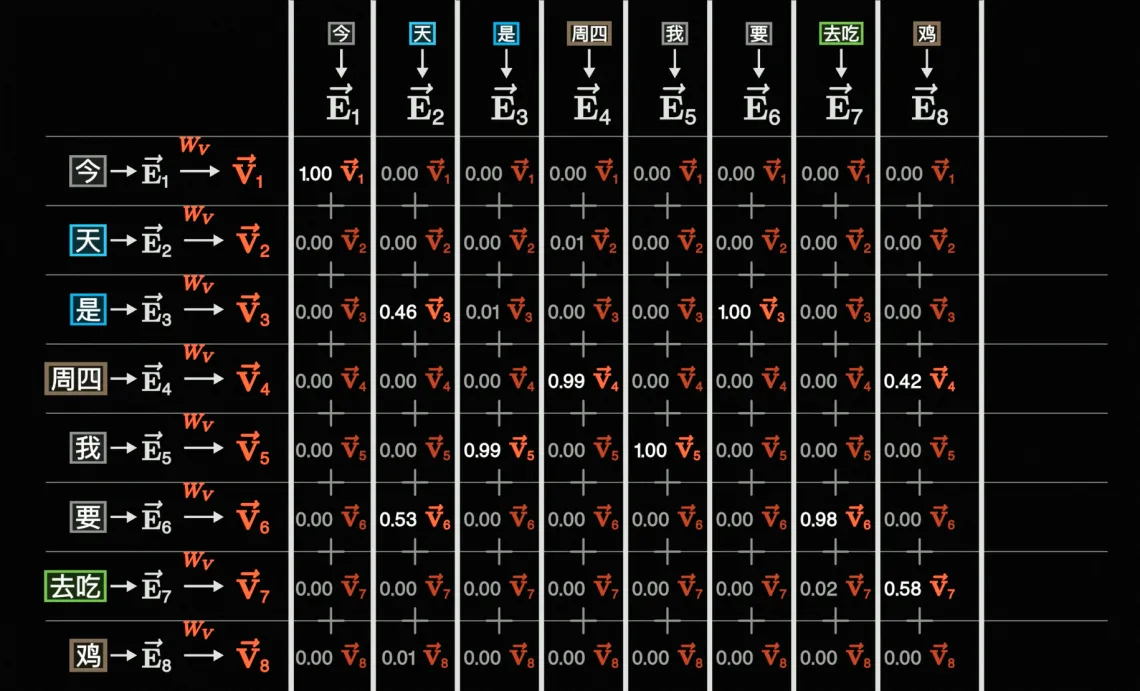
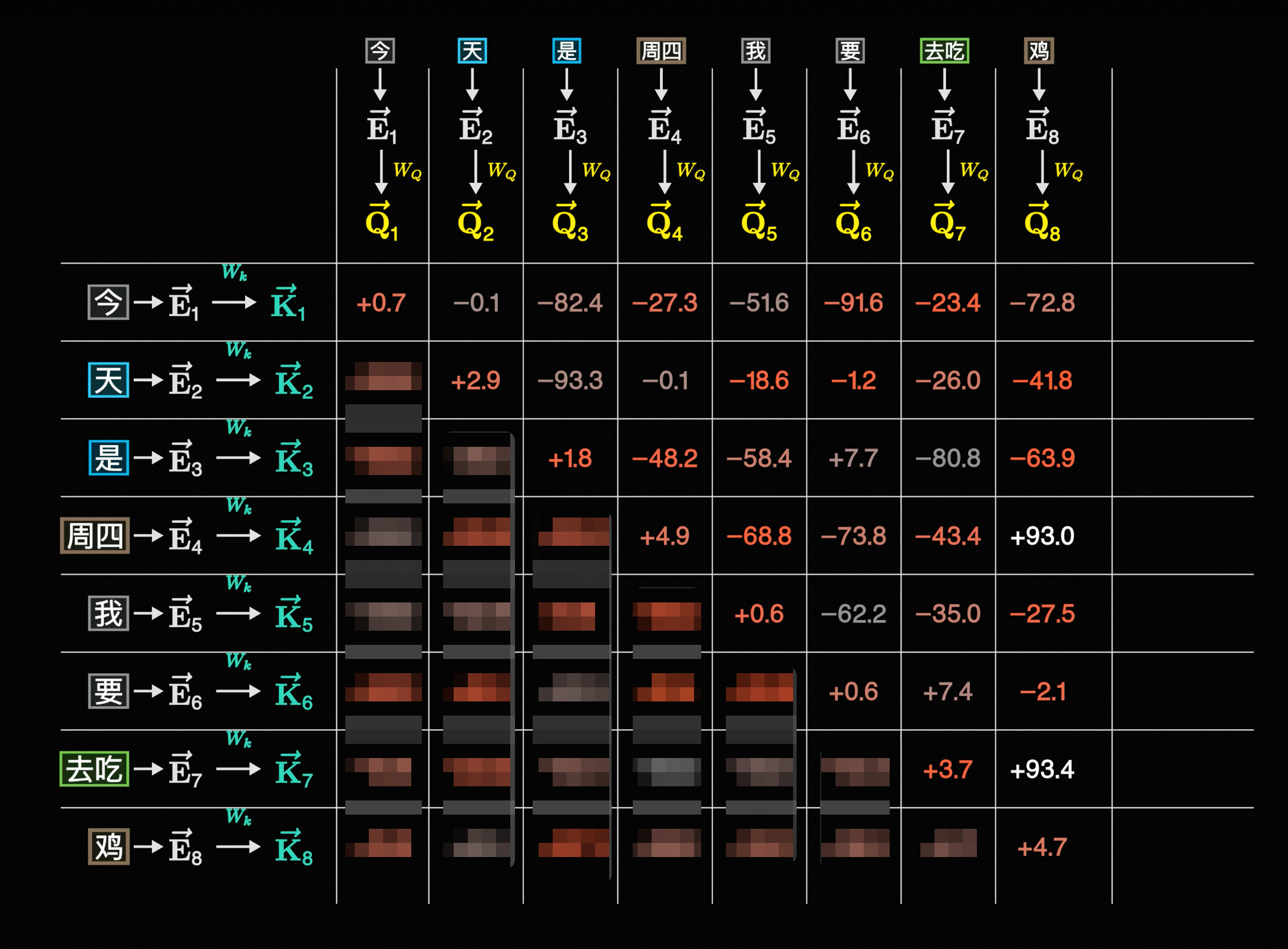
另外， $W_Q、W_K、W_V$ 这三个矩阵实际上也是要训练的，你可以理解为这三个矩阵一开始是随机值，一开始向量透过这个随机的矩阵后得到 $\vec{Q}、\vec{K}$ 后，它们点击结果可能会不太符合预期，比如下面这样：
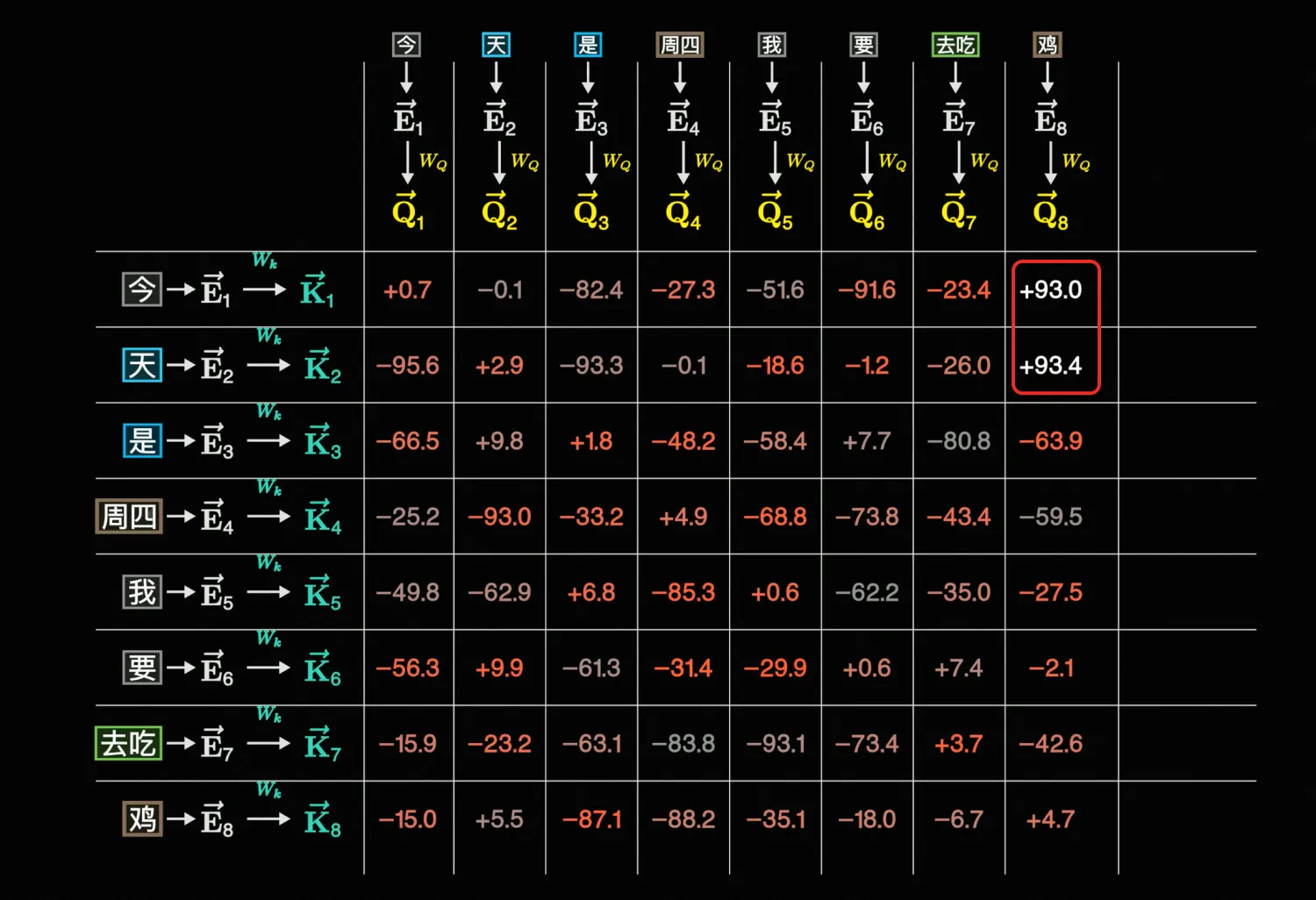
- 「鸡」跟「今」和「天」的点积结果大，表示它们关联性大，显然不正确
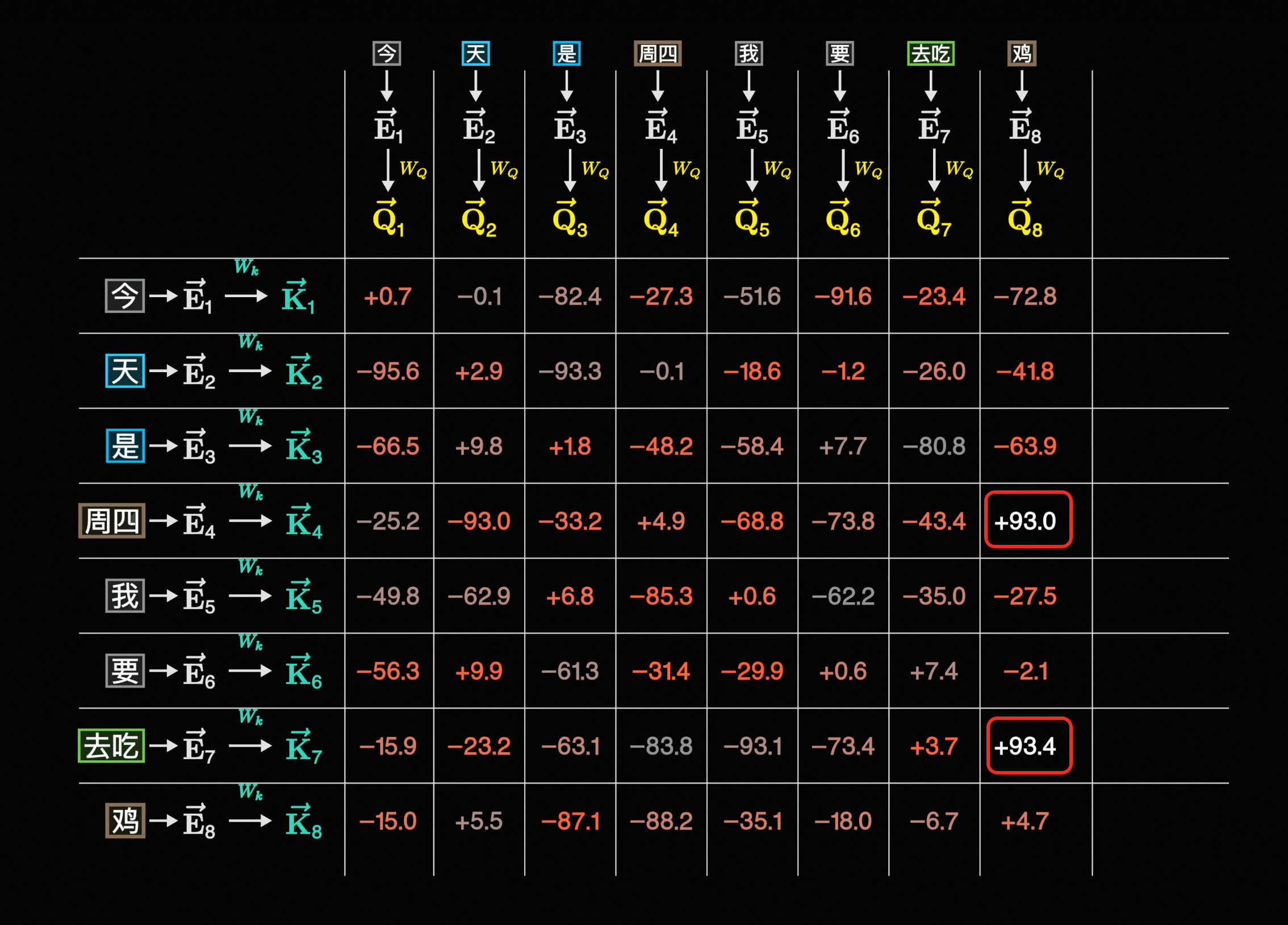
而经过Lose计算（比「衡量好坏」更复杂的算法）->反向传播梯度下降后（也就是训练后）， $W_Q、W_K、W_V$ 会发生变化，进而得到的 $\vec{Q}、\vec{K}、\vec{V}$ 也会发生变化，这时候点积的结果可能就比较符合预期了，比如下面这样：
总之，到这一步为止，我们就是在计算不同 $\vec{Q}、\vec{K}$ 的关联，计算出来的值也叫注意力分数

通俗理解QK点积

🦀 如果你已经完全理解QK点积的含义了，可以直接SKIP

在说V和softmax之前，可能还有人不明白为啥要拆成QK点积，比如上面的计算过程你可能都懂，但就是不明白为什么要这样做
如果你有这样的疑惑，这里首先建议把Q看成提问，而K当做关联信息
以下是一个我想出来比较通俗的case：
- 某天你回到家门口，发现新买的零食大礼包到了，但是上面裹了一层厚厚的胶带
- 这时候你会想：我要如何解开这层厚厚的胶带呢（ $\vec{Q_1}$ ）
- 你回到房间，目光扫过了房间的一些物品：车钥匙（ $\vec{K_1}$ ），一支笔（ $\vec{K_2}$ ），一把剪刀（ $\vec{K_3}$ ）
- 此时发现笔离你最近（ $\vec{Q_1} \cdot \vec{K_2}$ 结果大）
- 但你发现使用笔，解决不了这个问题（ ${Lose}$ 比较大）
- 于是你换成了剪刀，成功解决的胶带（预测正确， $Lose$ ↓）
- 下次再遇到这种情况你就知道要直接选剪刀了（ $W_Q、W_K、W_V$ 矩阵更新， $\vec{Q_1} \cdot \vec{K_3}$ 结果变大）
整个训练过程其实就像人类试错，只是有很多潜意识的动作我们平时自己也不会注意到

注意力Softmax & Temperature

上面提到过两个向量点积后，会得到一个注意力分数，但这个分数本质上是矩阵计算后的结果，它的范围是无限大的[-♾️, +♾️]，这可能导致梯度爆炸/梯度消失

关于梯度爆炸/梯度消失的内容，这里就简单概括一下：

梯度爆炸：如果出现一个极大正值，在神经网络的"套娃"下，这个数值会以指数级别增长，最终会导致"斜率"特别大，模型的学习一下子从"走路"变成"超光速"了，在终点面前总是跑过头，无法收敛
梯度消失：如果出现负值，则可能被激活函数"抹平"了（如ReLU的<0部分），最终会导致"斜率"特别小，模型的学习就会变得像是在平地上滑滑梯一样，根本滑不动（学习停滞）

如果忘记怎么个"套娃"法的，可以回去看上面「向量/矩阵化」小节；
如果是ReLU函数图像忘了，可以回顾下「非线性问题 + 激活函数」小节；

解决上述问题的方法之一，正是softmax，如果把注意力分数的向量写作 $\vec{\alpha} = \left[ \begin{matrix} \alpha_1 & \alpha_i \end{matrix} \right]$ ，它的公式是：

\text{softmax}(\alpha_i) = \frac{e^{\alpha_i}}{\sum_{j=1}^{n} e^{\alpha_j}}

第一次看到这个公式你可能会觉得叽里咕噜说啥呢，这里先简述一下softmax的作用：它吸收一个序列（行/列向量），然后把每个值映射到[0,1]区间，并且使所有映射后的值加起来=1
或许上面这段话讲起来太干，你可以自己调试一下下面这段代码：

python

01
02
03
04
05
06
07
08
09
10
11
12
13
if __name__ == '__main__':
    # import os
    # os.system('manim -pql softmax_demo.py visualizeSoftmax')

    import numpy as np
    import torch
    A = np.array(
      # [[99, 80, 90], [20, 50, 70], [0, 0, 0], [-99, -88, -999]],
      [[1, 1, 1], [2, 3, 4], [3, 3, 3], [-1, -1, -1]],
      dtype=np.float32
      # dtype=np.float64
    )
    after_softmax_tensor = torch.nn.functional.softmax(torch.from_numpy(A), dim=0)
    print(after_softmax_tensor)

上面输入的张量其实就相当于一个矩阵：

\begin{bmatrix} 1 & 1 & 1 \\[1em] 2 & 3 & 4 \\[1em] 3 & 3 & 3 \\[1em] -1 & -1 & -1 \\ \end{bmatrix}

经过softmax得到的输出是：

01
02
03
04
05
06
[
  [0.0889, 0.0628, 0.0350],
  [0.2418, 0.4643, 0.7020],
  [0.6572, 0.4643, 0.2583],
  [0.0120, 0.0085, 0.0047]
  // 每一列的和都≈1
]

而如果这个原本的数值相差比较大，则可能因为精度问题产生如下结果：

01
02
03
04
05
06
07
08
09
代码输入张量换成 → [[99, 80, 90], [20, 50, 70], [0, 0, 0], [-99, -88, -999]]

输出：
[
  [1.0000e+00, 1.0000e+00, 1.0000e+00],
  [4.9061e-35, 9.3576e-14, 2.0612e-09],
  [1.0089e-43, 1.8049e-35, 8.1940e-40],
  [0.0000e+00, 0.0000e+00, 0.0000e+00]
  // 虽然有一些变化，但每一列的和依旧≈1
]

Softmax把数值压到这个区间有什么意义呢？实际上这可以表示概率，比如0.9就是90%的概率；也可以表示权重，比如你KR中，KR1的权重是0.5，KR2的权重是0.3，KR3的权重是0.2等等
建议在注意力层把softmax的输出理解为权重，Transformer架构最后的softmax才理解成概率

Softmax虽然成功把注意力分数转成了概率/权重，但就上面的case而言[99, 80, 90]几乎是处于霸权地位，如果我们想让概率/权重的分布更加“均衡”，要怎么办呢？
其实增加一个底数就可以，这个参数通常叫做Temperature，调整Temperature会给结果带来如下变化：
如果你使用过一些开源的平台，或者公司内网的AI平台，应该会经常看到这个参数：
说个题外话，我公司的AI平台会把Temperature翻译成惊喜值，给人一种这个值越大越好的错觉，但如果你在工程里面把Temperature调大调小要看具体的场景：
- 比如你用大模型帮你做某种范围筛选/按照某种格式输出一类工作时，我建议把Temperature理解成"惊吓值"，通常这种情况是把Temperature设置为0提升输出稳定性
- 当然，也有调大的时候，最终取决于你的实验结果

V的作用 & 残差连接

视角重新回到计算出注意力得分，softmax前后的变化：
softmax前
softmax后
按照原来的公式，接下来要乘以一个 $V$ ：

softmax(\frac{QK^{T}}{\sqrt{d_k}})V

画成表格其实就是就是下面这样：
嗯，都是简单的加法和乘法，让一个初中生甚至小学生来都会算；但，你难免会问：为什么要这样算？这样算到底有什么意义？就像弱智吧吧友每句话里的字你都认得，但组合起来就不知道是啥了🤣

🍄 这段就当是个人碎碎念，看不懂可以放心SKIP

我初次遇到这个公式，因为会一点图形的皮毛，所以V前面哪部分基本是秒懂，感觉上有点类似于经过一通运算后，需要Normalize/Clamp(Input, 0, 1)一次，否则后续计算就可能都是做无用功：
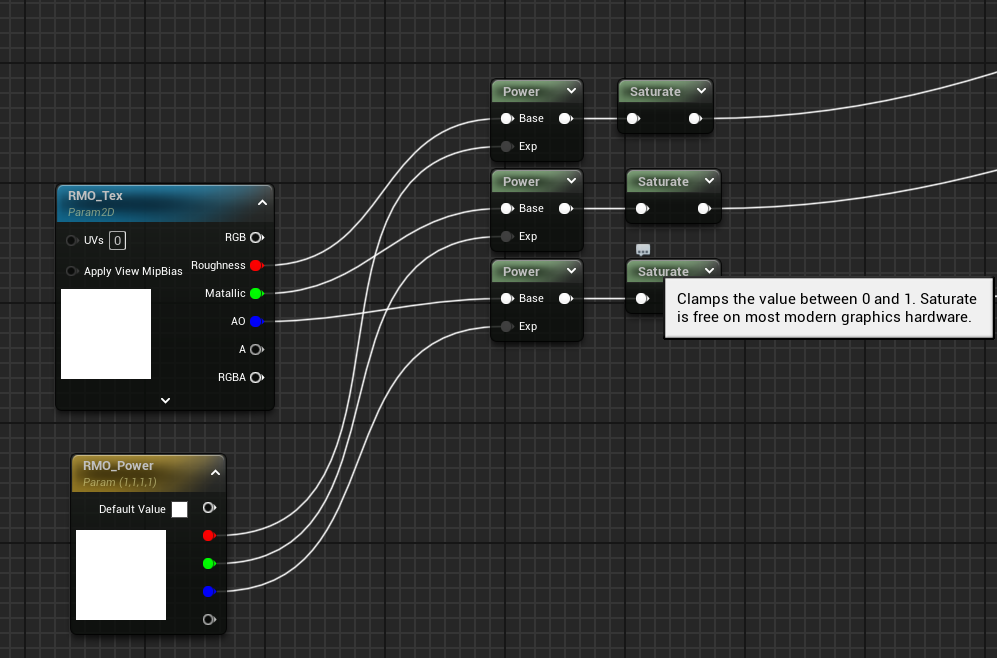
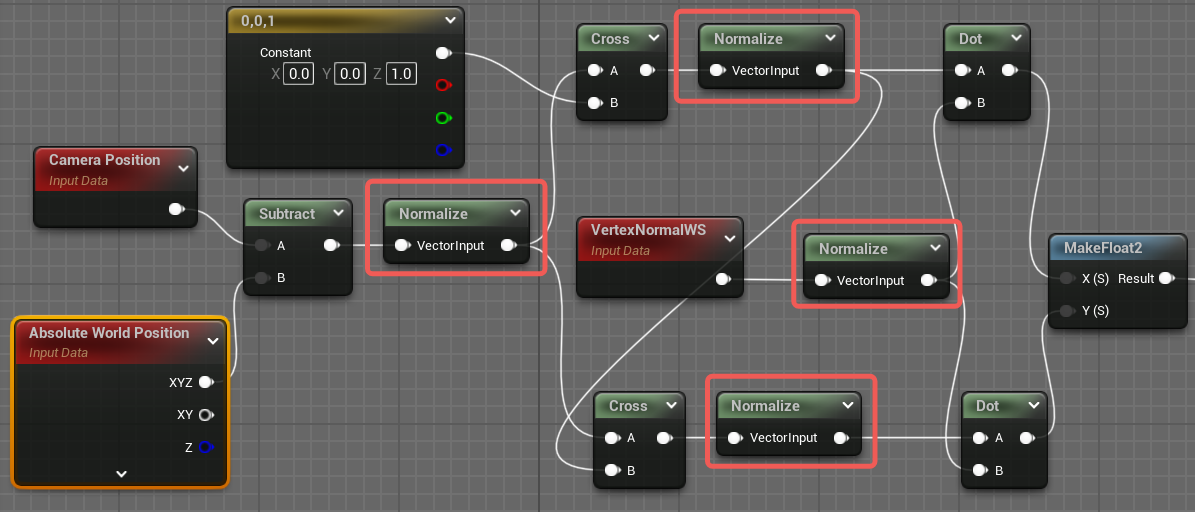
但到乘以V这一步，确实把我硬控了一段时间，我知道这也是一种加权求和，并且结果是某个"东西"，但就是不理解这个"东西"是干啥的，于是我开始检查softmax里面是不是有什么东西漏了、还是说点积理解错了等等
总之最后盯着这公式翻了半天资料，也找了一些资料看，但最后都没有结果，直到我的目光......

实际上我前面已经埋了不少伏笔了= =，要了解注意力权重 * V的作用，我们得把目光投射回Transformer的整体架构上，并且看看注意力计算后是什么：
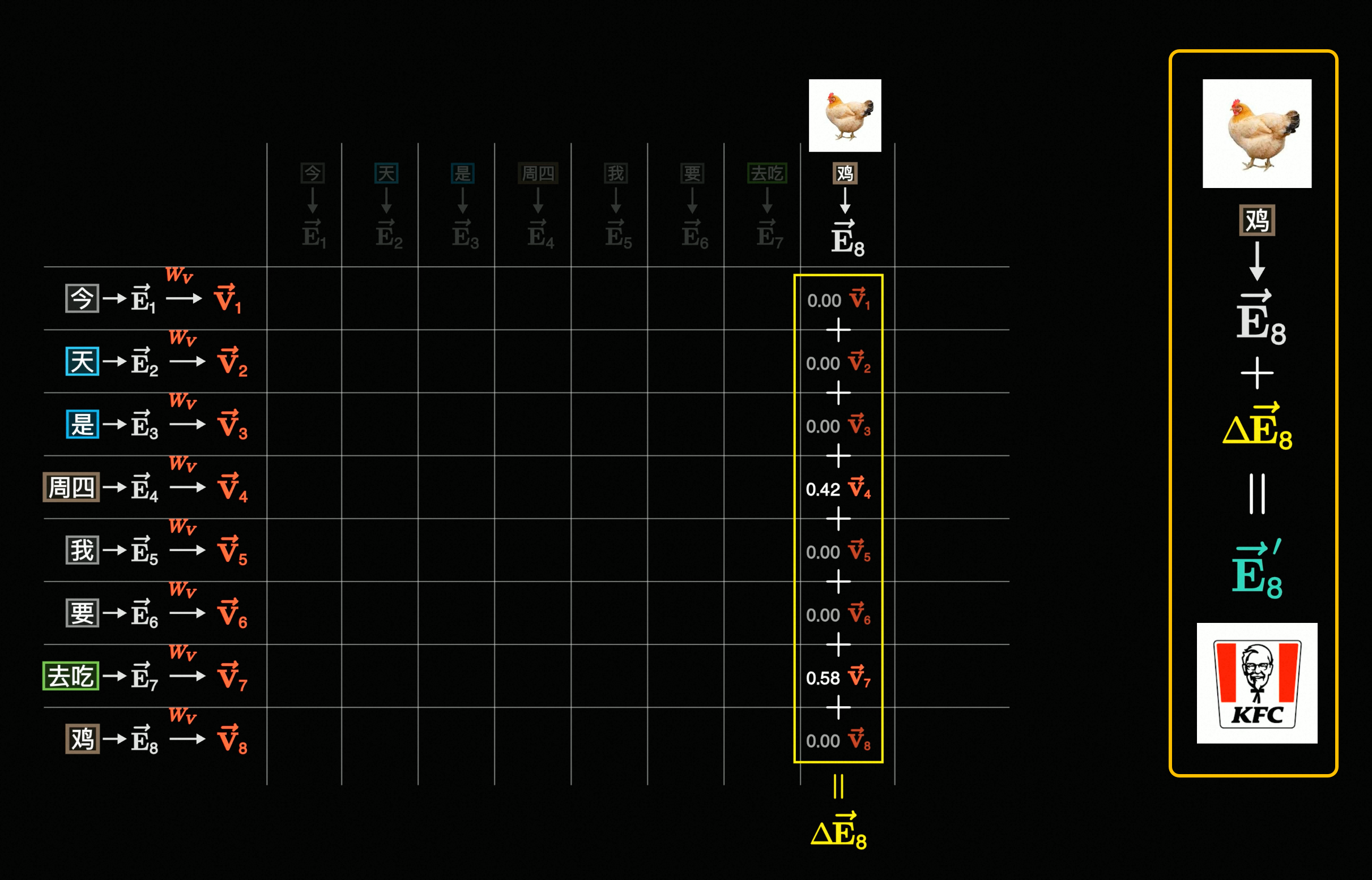
没错，有个Add，这个Add的步骤就是所谓的残差连接，并且根据图中箭头走向，发现是原始矩阵 + 注意力后矩阵，到这里其实一切都开始变得明朗起来了
为了方便理解大可不必上来就看整个矩阵相加有什么意义，可以先先从向量开始，前面提到过一个Token经过Embedding后会变成 $\vec{E}$ ，而注意力后的输出设为 $\Delta{\vec{E}}$ ，它们两个相加的意义如下图所示：
实际上这个 $\Delta{\vec{E}}$ 就是在上面「嵌入空间 & 在这之后」小节提到的 $\vec{b}$ ，为了节约你的爬楼时间，我就把图片重新在这里放一遍：
相信到这里，你已经一定程度上理解QKV的作用了，整个自注意力过程其实就是在把单个词义通过关联上下文信息 → QK点积 → softmax归一化 → V加权求和 → 转化为最终要表达的语义

通俗理解QKV

🧀 同样，如果你已经完全理解为什么会有QKV，可以直接SKIP

类似于上面的「通俗理解QK点积」，这个小结的目的是争取通过一个更"语义化"的case，试图让还不太明白为啥要有QKV这三玩意儿的人再"理解"以下
假设有如下场景
- 背景：你跟广州的朋友星期四来到清远玩，附近商场晚上有一个绝地求生的活动，朋友说：今晚去吃鸡
- 你（模型）的视角：嘶，他说的吃鸡到底是什么意思？（ $\vec{Q_1}$ ）
- 你回想了如下线索：
  - 朋友是广州的（ $\vec{K_1}$ ）
  - 现在在清远（ $\vec{K_2}$ ）
  - 今天是星期四（ $\vec{K_3}$ ）
  - 绝地求生的活动（ $\vec{K_4}$ ）
- 由于每个线索都有可能，所以你试探性的作出回答：哦，好久没吃过清远的走地鸡了
  - 等效于： $\vec{E}(鸡) + softmax(\frac{Q K^{T}}{\sqrt{d_k}})V（其中清远权重最高） =走地鸡$
- 但你的朋友却回答：不，我是说要吃白切鸡
  - 这一步就相当于得到Lose，并梯度下降、反向传播来修正你这个人类模型
- 你在得到朋友回答后，恍然大悟，表示知道了
  - QKV矩阵+全神经网络权重都更新了
  - 此时： $\vec{E}(鸡) + softmax(\frac{Q K^{T}}{\sqrt{d_k}})V（其中广州权重最高） =白切鸡$

多头注意力（MHA）

上面虽然讲清楚了注意力机制，但这种方式实际上只是单头注意力，我们视角切回到论文架构，会发现还有如下两个要点：
右边decoder到目前为止还是先忽略，我们现在看Nx，这表示着注意力这块实际上要做N次
而单头注意力有个问题在于进行N次以后，你的 $W_Q、W_K、W_V$ 确实能很好的能识别到"周四"、"去吃"将"鸡"成功理解成"肯德基"了
但这往往意味着除了"周四"、"去吃"外的词，权重会变得越来越低，假如现在上文中还有"会唱"、"会跳"、"会rap"、"会打篮球"，你希望模型理解到的是：
但因为Nx层层堆叠后其它token不断降权，最后还是只保留了"周四"、"去吃"，因此模型依旧理解成了：
这显然是不符合预期的，为了解决这个问题，就有了多头注意力（也就是图中的Multi-Head Attention）
在这里，你可以简单地把多头注意力简单理解为每个头都会关注不同的特征/维度的含义：
每个注意力头都是单独的 $W_{Qi}、W_{Ki}、W_{Vi}$ 矩阵，这样就不会被其它注意力头的"降权"影响到了
当然，上面只是对多注意力头一个非常简化的解释，实际流程中还会把原来的一个头"降维切割"再分别计算，最终再做一次"加权求和"，但这里就不展开细节来讲了，怕分散你的注意力= =

FFN层作用

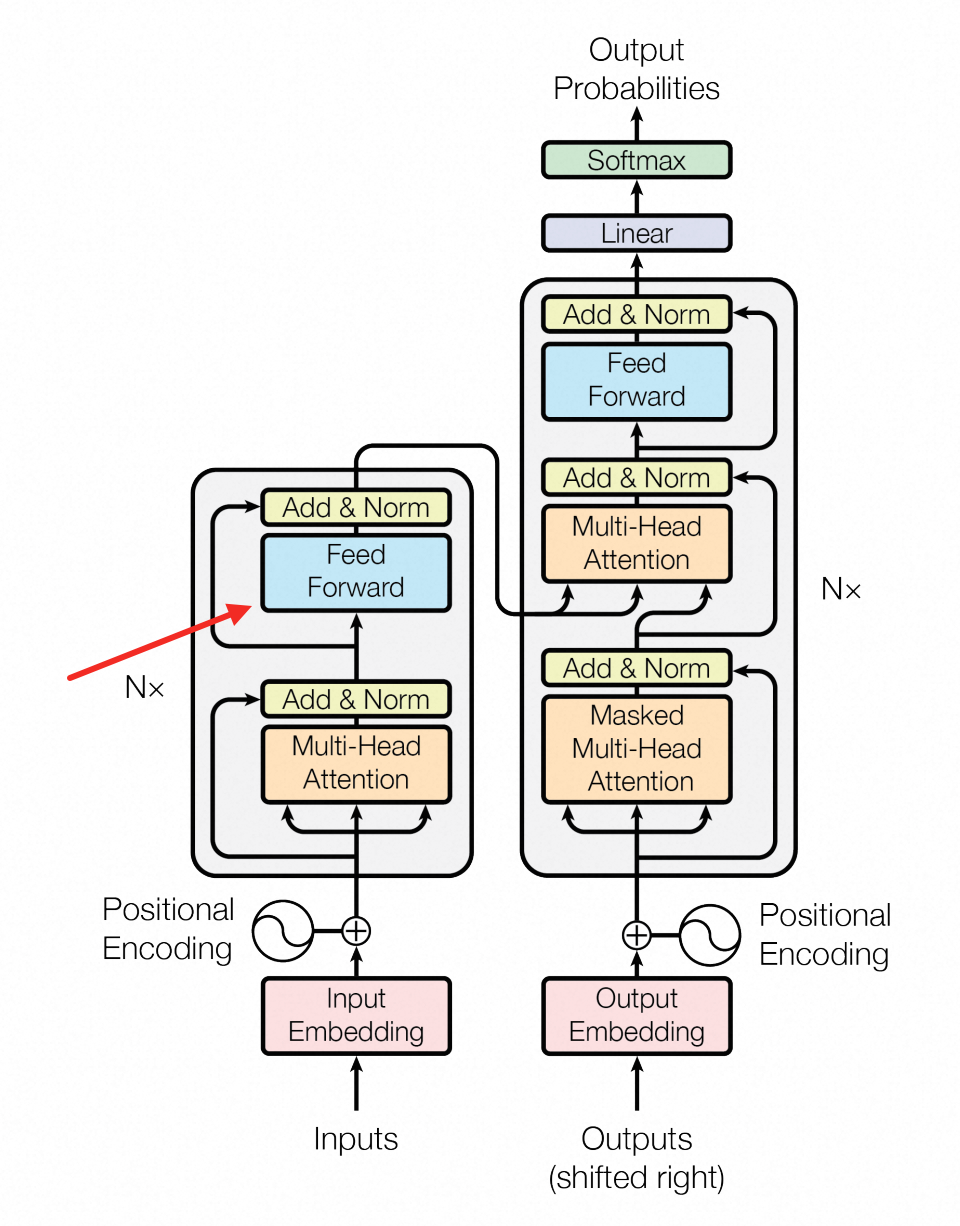
FFN讲的其实就是图中的Feed Forward部分：
论文中的全称是fully connected feed-forward network，稍微翻译一下就是全连接前向网络：
实际上它就是我们在「必要基础」章节提到的全连接神经网络，但因为各种历史原因，它可能还有别的名字，比如MLP等
上面稍微解释了下别名，但我想说的是：即便它还有1W+个别名，也不重要，重要的是它里面有什么；so，让我们瞧一瞧这个神经网络里面有啥：
好巧啊，上面「非线性问题 + 激活函数」小节我们正好讲的就是Transformer中使用到的ReLU激活函数
那么为什么要引入ReLU呢？原因是前面说到的所有的Embedding、注意力的运算全部都是线性运算，通过这种方式训练永远只能是"一条直线"，但理解语言本身并不是一个纯线性运算就能"拟合"的东西，所以需要引入激活函数来解决非线性的问题，这里再贴一次上面ReLU和纯线性(liner)的对比图
纯线性时
引入非线性后
实际上也有人试着把FFN这层去掉，结果就是准确率大幅下降变回智障，这也侧面说明了非线性的重要性

为什么会有encoder和decoder（交叉注意力）

前面的内容其实已经把encoder那一边的东西讲完了，要了解decoder我们得先了解一下Transformer在设计之初是用来干嘛的，以下是论文原文：
没错，Transformer设计之初并不是用于大模型，而是普普通通地完成翻译任务的模型，但实际上这个翻译不仅仅是停留在不同语言翻译的问题，更深层次地来说是在解决输入输出长度不一致下的如何计算的问题，这类问题统称为seq2seq问题，像文字转图片，文字转语音等等其实都是seq2seq问题
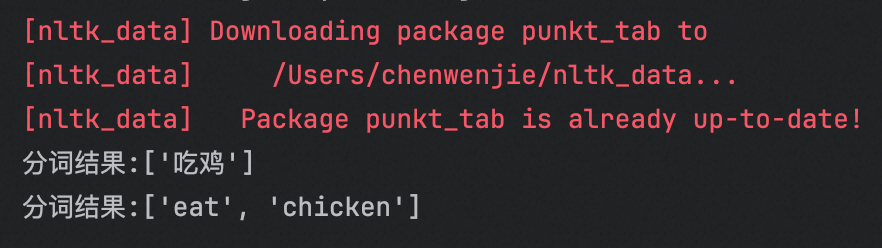
比如这里写一段对「吃鸡」和「eat chicken」分词的代码：

python

01
02
03
04
05
06
07
08
09
10
11
if __name__ == '__main__':

    import nltk
    nltk.download('punkt_tab')

    text = "吃鸡"
    tokens = nltk.word_tokenize(text)
    print("分词结果:" + str(tokens))

    text = "eat chicken"
    tokens = nltk.word_tokenize(text)
    print("分词结果:" + str(tokens))

输出结果如下，如果变成翻译问题，就是输入1个词「吃鸡」，翻译的输出会变成2个词「eat」「chicken」：
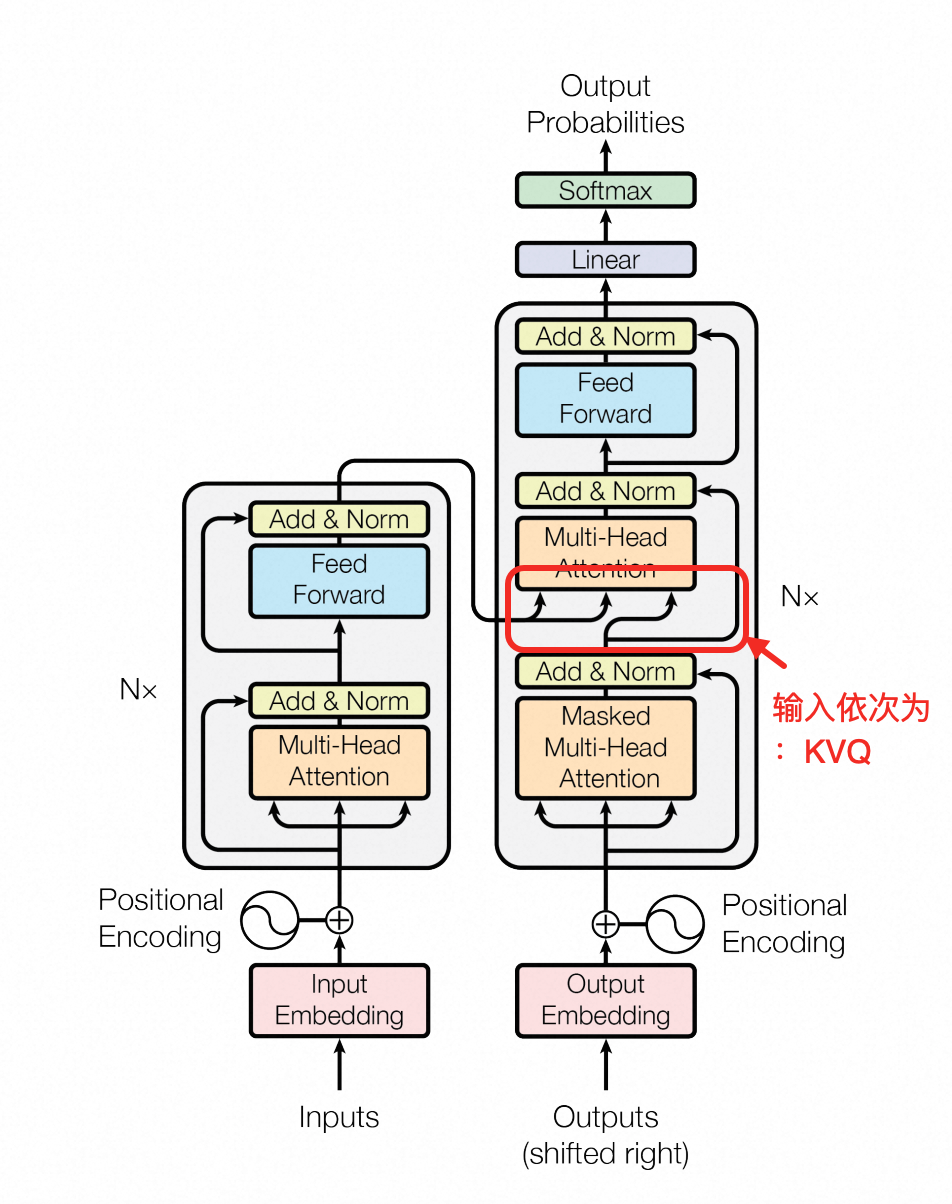
而解决输入输出长度不一致问题的方案就藏在decoder中：
上面红框部分其实就是交叉注意力（cross attention），作者的图也比较清楚地表达了输入的来源，比如计算注意力的KV来自于encoder，而Q来自于decoder，如果把公式稍微改改，就是下面这样：

CrossAttention(Q,K,V) = softmax(\frac{Q_{decoder}K_{encoder}^{T}}{\sqrt{d_k}})V_{encoder}

拉成点积计算的表格就是下面这样：
因为KV都来自encoder，后续计算出注意力分数后，V是可以1比1乘上去的，不会有任何问题，所以就不再赘述乘以V的过程了= =

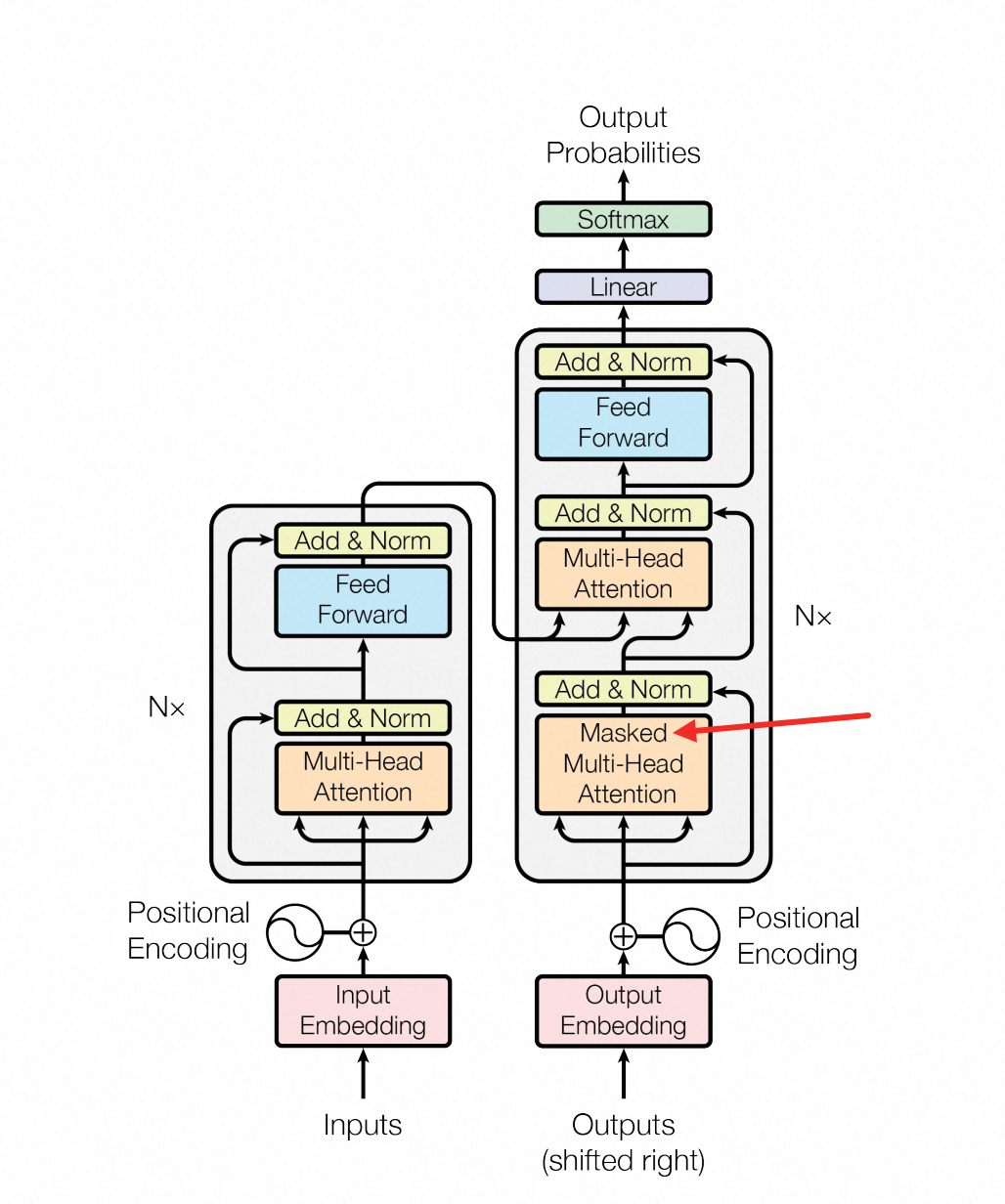
带掩码的注意力

细心的你，可能还会发现在上面交叉注意力之前，还有一个带"Masked"的注意力机制：
实际上这就是一个掩码（Masked），它的作用是“一个token”不能与"这个token后面"的东西计算注意力分数，如下图所示：
通俗一点说就是不让模型在训练时"偷看答案"，这其实也是一件很符合直觉的事情，如果都知道答案了，那还训练来干嘛🤣
那么这个掩码到底是怎么做的呢？还记得在「注意力Softmax & Temperature」小节中，提到过如果计算softmax前存在很大的负值，那么在softmax后因为精度丢失问题而变成0
而我们也可以利用这个思路，让注意力得分矩阵加上一个掩码矩阵，再进行sofmax：

softmax(\frac{Q K^{T}}{\sqrt{d_k}} + M_{mask})V \\[1em] \begin{bmatrix} 1.1 & 1.2 & 1.3 \\[1em] 2.2 & 2.3 & 2.4 \\[1em] 3.3 & 3.4 & 3.5 \\ \end{bmatrix} + \begin{bmatrix} 0 & 0 & 0 \\[1em] -\infty & 0 & 0 \\[1em] -\infty & -\infty & 0 \\ \end{bmatrix} = \begin{bmatrix} 1.1 & 1.2 & 1.3 \\[1em] -\infty & 2.3 & 2.3 \\[1em] -\infty & -\infty & 3.5 \\ \end{bmatrix} \\[1em] ↓ \\[1em] softmax \\[1em] ↓ \\[1em] \begin{bmatrix} 1.00 & 0.25 & 0.07 \\[1em] 0.00 & 0.75 & 0.23 \\[1em] 0.00 & 0.00 & 0.70 \\ \end{bmatrix}

你可以简单理解为：变成0的部分就是遮住的"答案"，因为就算没有它，每一列的和也都是1，就像不存在一样

砍掉encoder/decoder可以吗

当然可以，如果你能想到这一层，说明你的直觉非常正确 🎉
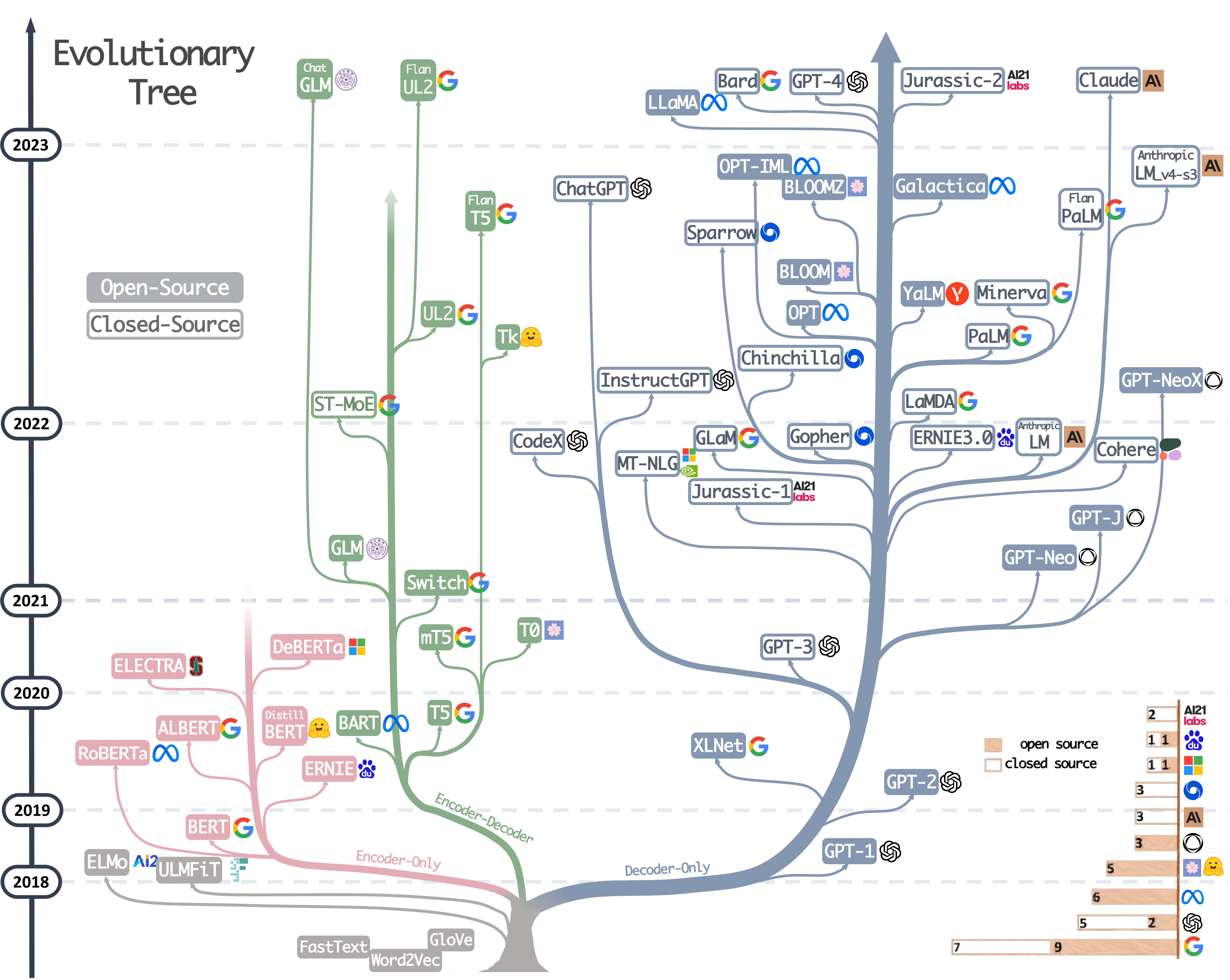
下图就是各类基于Transformer衍生出的模型，靠左是encoder-only靠右是decoder-only：
原始的Transformer模型分为encoder和decoder，分别用于处理输入和生成输出，类似「理解」与「表达」分工。而像GPT这样的模型，它的任务是按顺序生成文本内容，故仅保留解码器部分，将「理解」和「生成」合并到同一结构中，这种仅用解码器的方式就是所谓的decoder-only
附上一些参考资料，感兴趣的可以继续往下探究：
- https://github.com/Mooler0410/LLMsPracticalGuide（上面图出自这里）
- 为什么现在的LLM都是Decoder only的架构？

Transformer的"最后"

到目前为止，就只剩下一个问题了：经过重重计算后的词向量，如何转成下一个词输出的概率？
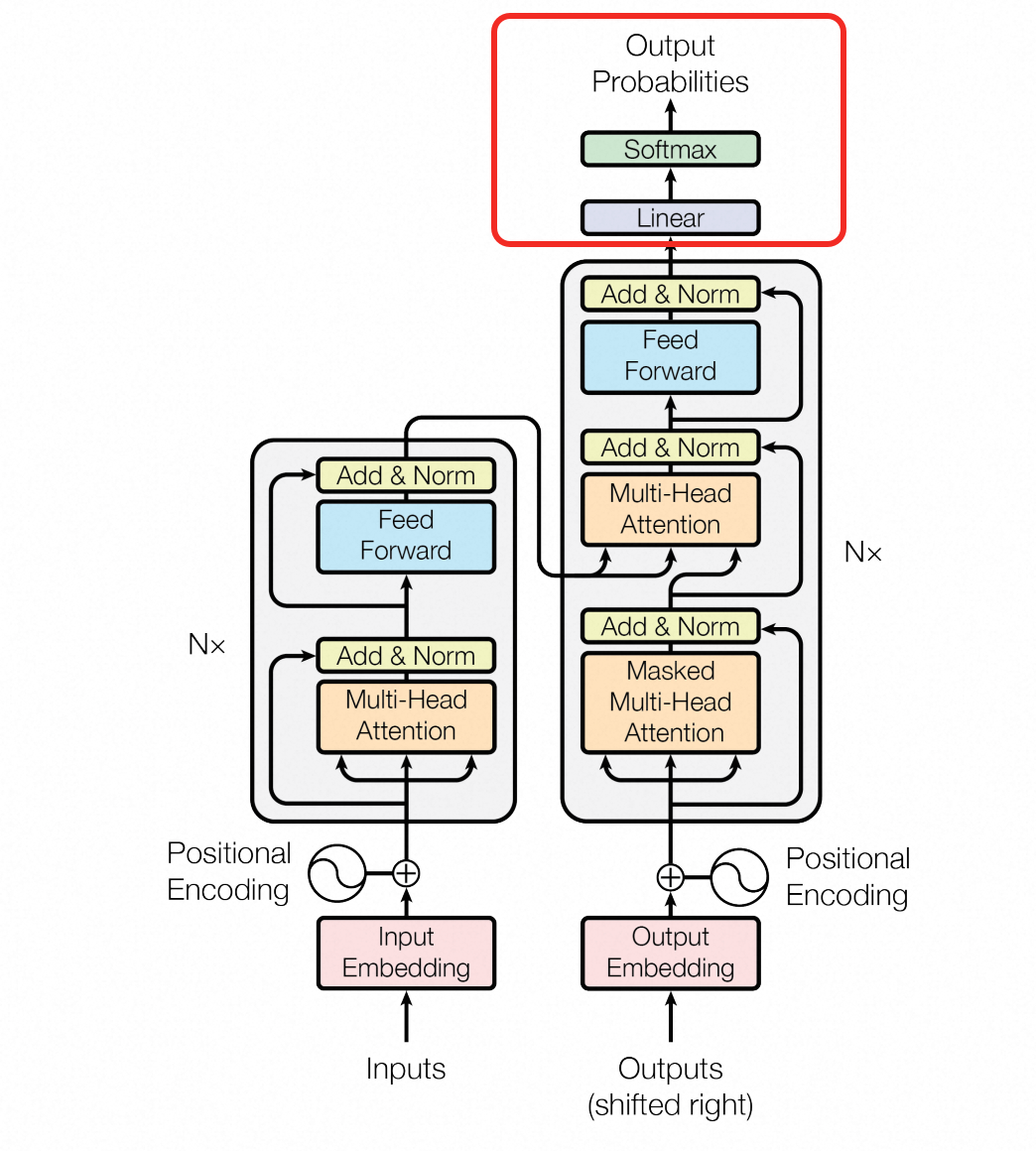
这其实就是交叉注意力+FFN后，所做的事情（红框部分）：
这里的Linear其实也可以看作是一个非常简单是一个神经网络，只不过里面没有激活函数，只能做线性变换，才取名叫Linear
不过需要注意的是，Linear层在训练模式-还在训练过程和推理模式-训练完成后的对话下做的事情可能不太一样
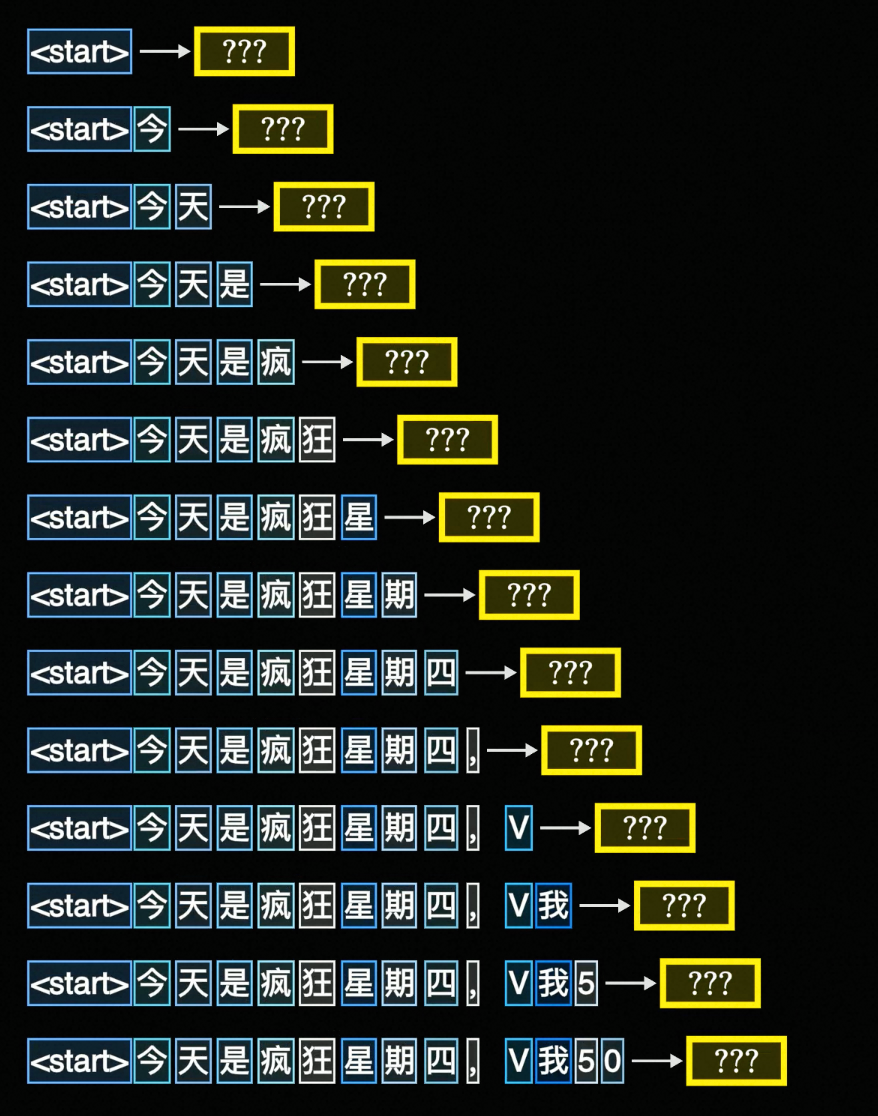
首先是训练模式下，是将输入的文本拆分，然后并行地预测（<start>是起始符）：
而在推理模式中，只会取最后一个token做下一个toekn的预测，因为最后一个token可以看作是融合了所有上文得到的产物
后文中，我只讲推理模式下Linear到底做了什么，毕竟看这篇文章的应该是纯使用者居多

还记得前几段文字中提到Linear就是一个无激活函数的神经网络吗，我们在更前面的内容中学过神经网络的本质就是wx+b，而这里暂时忽略掉b，变成wx
在「Embedding的由来」小节中提到过，词向量是词汇表"降维"得来的，而这里的Linear其实还肩负着把词向量给"升维回去"，变回跟词汇表相同大小维度的作用
那么怎么升维呢，这里需要再补充一个矩阵乘法的小知识：

{矩阵}_{\textcolor{red}{Z \times M}} \times {矩阵}_{\textcolor{red}{M \times N}} \rightarrow {矩阵}_{\textcolor{red}{Z \times N}} \\[1em] ↓ \\[1em] 词向量为1\times2，升维矩阵为2\times3，升维后得到1\times3 \\[1em] ↓ \\[1em] \begin{bmatrix} 1 & 2 \end{bmatrix} \times \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6\\ \end{bmatrix} = \begin{bmatrix} 1\times1+2\times4 & 1\times2+2\times5 & 1\times3+2\times6 \end{bmatrix} = \begin{bmatrix} 9 & 12 & 15 \end{bmatrix}

这个升维的过程本质就是wx，w是一个矩阵，x是词向量，不过这里的w并不是一个新的训练参数而是一个共享参数，它实际上是Embedding阶段嵌入矩阵的转置，暂且记为 $W_{embedding}^{T}$
- 这其实也非常符合直觉，毕竟如果是一个新的训练参数，到最后我们还怎么把向量还原成文字输出呢= =
你可以把 $W_{embedding}^{T}$ 看做是一词汇表长度 X 512的矩阵如果说原本词向量512 X 1 ，那么相乘后，就变词汇表长度 X 1的矩阵了
下面展示取最后一个token经过Linear和softmax后得到概率的过程：
得到每个id的概率之后，后续还会根据束搜索 or 各种采样算法，获取结果id，最终拿结果id到map取出来，就变成要生成的字了
transformer之旅到此结束~

其它QA（题外话）

为什么不根据语法学习

相信绝大部分人在学英语/其它外语的时候，第一件事是认单词，第二件事就是学语法，比如主谓宾
那为什么不让机器也按照这种思路去学习呢？实际上有人做过相关的研究，但纯粹靠语法，难免会生成一些语法正确但完全不合理的东西，比如某个同时的微信昵称：
躁动的黄鸡蛋从语法上讲名词+形容词的组合完全正确，但实际语义没人能看懂，我曾一度怀疑这个昵称是不是用某种AI生成的🤣

为什么transformer能受欢迎

我个人觉得主要归功于2点：
- 并行性好：意味着可以轻松突破原来数据规模的限制，并且速度更快
- 可移植性好：可以用于自然语言、图像、语音等领域，一个领域有成果，可快速移植到别的领域
实际上论文原文中也有提到：
而后续各种领域大模型井喷式涌出的现象，也正如论文预测那般美好

核心参考、工具

文章内容核心参考：3b1b（yyds）
- 反正贴一大堆论文非算法人估计也不会去看
画图/动画工具：
- manim-3b1b version、manim-ce version
- draw.io
- GeoGebra Classic 6-桌面版（在线有个老版本的bug坑死人）
- ppt（向量部分拿games101的ppt改了下）

如果觉得文章对你有用，请随意赞赏

杂谈心得

非算法人-从神经网络到Transformer

https://wenjie.store/archives/zero-2-transformer

作者

WenJie

发布于

2025-04-13

更新于

2025-04-23

许可协议

CC BY 4.0

非算法人-从神经网络到Transformer

前言

必要基础

从预测酒店销量开始

衡量好坏

梯度下降

局部最优和全局最优

非线性问题 + 激活函数

神经元与神经网络

小扩展

向量/矩阵化

如何理解提升维度能解更多问题

Transformer

矩阵基础

向量基础

Embedding的由来

嵌入空间 & 在这之后

Transformer结构预览

自注意力机制（self-attention）

通俗理解QK点积

注意力Softmax & Temperature

V的作用 & 残差连接

通俗理解QKV

多头注意力（MHA）

FFN层作用

为什么会有encoder和decoder（交叉注意力）

带掩码的注意力

砍掉encoder/decoder可以吗

Transformer的"最后"

其它QA（题外话）

为什么不根据语法学习

为什么transformer能受欢迎

核心参考、工具

作者

发布于

更新于

许可协议

微信扫一扫：分享

评论